Giải bài tập toán lớp 8 kết nối tri thức bài 6 Hiệu hai bình phương. Bình phương của một tổng hay một hiệu

1. Hằng đẳng thức

Luyện tập 1 trang 30 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Trong các đẳng thức sau, đẳng thức nào là hằng đẳng thức?

a) $a(a+2b)=a^{2}+2ab$

b) a + 1 = 3a - 1

2. Hiệu hai bình phương

Hoạt động 1 trang 30 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Quan sát hình 2.1.

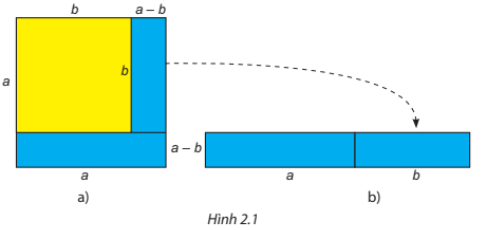
a) Tính diện tích của phần hình màu xanh ở hình 2.1a

b) Tính diện tích hình chữ nhật màu xanh ở hình 2.1b

c) Có nhận xét gì về diện tích của hai hình ở câu a và câu b

Hoạt động 2 trang 31 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Với hai số a, b bất kì, thực hiện phép tính $(a+b)\times (a-b)$

Từ đó rút ra liên hệ giữa $a^{2}-b^{2}$ và (a + b)(a - b)

Luyện tập 2 trang 31 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: 

a) Tính nhanh $99^{2}-1$

b) Viết $(x^{2}-9)$ dưới dạng tích

3. Bình phương của một tổng

Hoạt động 3 trang 31 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Với hai số a, b bất kì, thực hiện phép tính (a + b)(a + b)

Từ đó rút ra liên hệ giữa $(a+b)^{2}$ và $a^{2}+2ab+b^{2}$

Luyện tập 3 trang 32 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: 

1. Khai triển $(2b+1)^{2}$
2. Viết biểu thức $9y^{2}+6yx+x^{2}$ dưới dạng bình phương của một tổng

4. Bình phương của một hiệu

Hoạt động 4 trang 32 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Với hai số a, b bất kì. biết a -b = a +(-b) và áp dụng hằng đẳng thức của một tổng để tính $(a-b)^{2}$

Luyện tập 4 trang 32 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Khai triển $(3x-2y)^{2}$

Bài tập

Bài tập 2.1 trang 30 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Những đẳng thức nào sau đây là hằng đẳng thức?

a) x + 2 = 3x + 1

b) $2x(x+1)=2x^{2}+2x$

c) $(a+b)a=a^{2}+ba$

d) a - 2 = 2a + 1

Bài tập 2.2 trang 33 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Thay ? bằng biểu thức thích hợp.

a) $x-3y)(x+3y)=x^{2}-?$

b) $(2x-y)(2x+y)=4?-y^{2}$

c) $x^{2}+8xy+?=(?+4y)^{2}$

d) $?-12xy+9y^{2}=(2x-?)^{2}$

Bài tập 2.3 trang 33 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Tính nhanh

a) 54 x 66

b) $203^{2}$

Bài tập 2.4 trang 33 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu

a) $x^{2}+4x+4$

b) $16a^{2}-16ab+4b^{2}$

Bài tập 2.5 trang 33 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Rút gọn các biểu thức sau:

a) $(x-3y)^{2}-(x+3y)^{2}$

b) $(3x+4y)^{2}+(4x-3y)^{2}$

Bài tập 2.6 trang 33 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Chứng minh rằng với mọi số tự nhiên n, ta có:

$(n+2)^{2}-n^{2}$ chia hết cho 4