Giải bài tập toán lớp 8 kết nối tri thức bài Luyện tập chung trang 73

Trong sách Giải bài tập toán lớp 8 kết nối tri thức, trang 73 là phần Luyện tập chung. Bài này cung cấp đầy đủ đáp án chuẩn và hướng dẫn giải chi tiết cho từng bài tập trong chương trình học. Đây là cơ hội để học sinh nắm vững kiến thức và hiểu rõ hơn về bài học.

Qua việc giải bài tập trang 73, các em học sinh sẽ có cơ hội nâng cao kỹ năng toán học của mình. Bằng cách tự mình giải quyết các bài tập, họ sẽ hiểu sâu hơn về lý thuyết và áp dụng kiến thức vào thực tế.

Hy vọng rằng việc học và giải bài tập từ sách Giải toán lớp 8 sẽ giúp các em phát triển tư duy logic và trí tuệ toán học, từ đó đạt được kết quả tốt trong môn học này.

Bài tập và hướng dẫn giải

Bài tập

Bài tập 3.34 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn MP

a) Hỏi tứ giác AMCP là hình gì? Vì sao?

b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông?

Trả lời: Để giải bài toán trên, ta có thể dùng phương pháp sau:a) Ta có NA = NC (do N là trung điểm của AC),... Xem hướng dẫn giải chi tiết

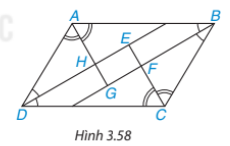
Bài tập 3.35 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữu nhật.

Giải Bài tập 3.35 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 Kết nối

Trả lời: Phương pháp giải:Gọi M, N, P, Q lần lượt là giao điểm của các đường phân giác với các cạnh của hình... Xem hướng dẫn giải chi tiết

Bài tập 3.36 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Một khung tre hình chữ nhật có lắp đinh vít tại bốn đỉnh. Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình gì? Tại sao? Hỏi khi nẹp thêm một đường chéo vào khung đó thì nó còn bị xô lệch không?

Trả lời: Phương pháp giải:Để giải bài toán này, ta cần xem xét tính chất của hình chữ nhật và hình bình hành.... Xem hướng dẫn giải chi tiết

Bài tập 3.37 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x'Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?

Trả lời: Để giải bài toán này, ta sẽ áp dụng các kiến thức về góc phân giác và hình chữ nhật.Phương pháp... Xem hướng dẫn giải chi tiết

Bài tập 3.38 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho hình vuông ABCD. Lấy một điểm E trên cạnh CD. Tia phân giác của góc DAE cắt cạnh DC tại M. Đường thẳng qua M vuông góc với AE cắt BC tại N. Chứng minh DM + BN = MN

Trả lời: Để chứng minh DM + BN = MN, ta xét tam giác AMD và tam giác AMN.- Ta có AM chung.- $\widehat{AMH} =... Xem hướng dẫn giải chi tiết

Giải bài tập liên quan khác

CHƯƠNG I: ĐA THỨC

CHƯƠNG II: HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG

CHƯƠNG III: TỨ GIÁC

CHƯƠNG IV: ĐỊNH LÍ THALES

CHƯƠNG V: DỮ LIỆU VÀ BIỂU ĐỒ

CHƯƠNG VI. PHÂN THỨC ĐẠI SỐ

CHƯƠNG VII. PHƯƠNG TRÌNH BẬC NHẤT VÀ HÀM SỐ BẬC NHẤT

CHƯƠNG VIII. MỞ ĐẦU VỀ TÍNH XÁC SUẤT CỦA BIẾN CỐ

CHƯƠNG IX. TAM GIÁC ĐỒNG DẠNG

CHƯƠNG X. MỘT SỐ HÌNH KHỐI TRONG THỰC TIẾN

Giải bài tập toán lớp 8 kết nối tri thức bài Luyện tập chung trang 73