Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài Bài tập cuối chương V

Bài 1 : Cho hình chữ nhật ABCD có AB = 3, BC = 4. Độ dài của vectơ AC là:

A. 5;

B. 6;

C. 7;

D. 9.

Bài 2 : Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ OC có điểm đầu và điểm cuối là các đỉnh lục giác là:

A. 2;

B. 3;

C. 4;

D. 6.

Bài 3 : Cho ba điểm phân biệt A, B, C. Khẳng định nào sau đây là đúng?

A. $\overrightarrow{CA}$ - $\overrightarrow{BA}$ = $\overrightarrow{BC}$ ;

B. $\overrightarrow{AB}$ + $\overrightarrow{BA}$ = $\overrightarrow{BC}$ ;

C. $\overrightarrow{AB}$ + $\overrightarrow{CA}$ = $\overrightarrow{CB}$ ;

D. $\overrightarrow{AB}$ - $\overrightarrow{BC}$ = $\overrightarrow{CA}$ .

Bài 4 : Cho hai điểm phân biệt A và B. Điều kiện để điểm Ià trung điểm của đoạn thẳng AB là:

A. IA = IB ;

B. $\overrightarrow{IA}$ = $\overrightarrow{IB}$ ;

C. $\overrightarrow{IA}$ = -$\overrightarrow{IB}$ ;

D. $\overrightarrow{AI}$ = $\overrightarrow{BI}$ .

Bài 5 : Cho tam giác ABC có G là trọng tâm và I là trung điểm của đoạn thẳng BC. Khẳng định nào sau đây là đúng?

A. $\overrightarrow{GA}$ = 2$\overrightarrow{GI}$ ;

B. $\overrightarrow{GI}$ = $\frac{-1}{3}$ $\overrightarrow{IA}$ ;

C. $\overrightarrow{GA}$ + $\overrightarrow{GC}$ = 2$\overrightarrow{GI}$ ;

D. $\overrightarrow{GA}$ + $\overrightarrow{GC}$ = -$\overrightarrow{GA}$ .

Bài 6 : Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?

A. $\overrightarrow{AC}$ + $\overrightarrow{BD}$ = 2$\overrightarrow{BC}$ ;

B. $\overrightarrow{AC}$ + $\overrightarrow{BC}$ = $\overrightarrow{AB}$ ;

C. $\overrightarrow{AC}$ + $\overrightarrow{BD}$ = 2$\overrightarrow{CD}$ ;

D. $\overrightarrow{AC}$ + $\overrightarrow{AD}$ = $\overrightarrow{CD}$ .

Bài 7 : Cho tam giác ABC. Đặt $\overrightarrow{a}$ = $\overrightarrow{BC}$ ; $\overrightarrow{b}$ = $\overrightarrow{AC}$ . Các cặp vectơ nào sau đây cùng phương?

A. 2$\overrightarrow{a}$ + $\overrightarrow{b}$ và $\overrightarrow{a}$ + 2$\overrightarrow{b}$ ;

B. $\overrightarrow{AB}$ + $\overrightarrow{AB}$ và 2$\overrightarrow{a}$ - $\overrightarrow{b}$ ;

C. 5$\overrightarrow{a}$ + 2$\overrightarrow{b}$ và -10$\overrightarrow{a}$ - 2$\overrightarrow{b}$ ;

D. $\overrightarrow{a}$ + $\overrightarrow{b}$ và $\overrightarrow{a}$ - $\overrightarrow{b}$ .

Bài 8 : Tam giác ABC vuông ở A và có góc B = 50°. Khẳng định nào sau đây là sai?

A. ($\overrightarrow{AB}$ , $\overrightarrow{BC}$) = 130°;

B. ($\overrightarrow{BC}$ , $\overrightarrow{AC}$) = 40°;

C. ($\overrightarrow{AB}$ , $\overrightarrow{CB}$) = 50°;

D. ($\overrightarrow{AC}$ , $\overrightarrow{CB}$) = 120°.

Bài 9 : Cho vectơ a và vectơ b là hai vectơ cùng hướng và đều khác vectơ 0. Khẳng định nào sau đây là đúng ?

A. $\overrightarrow{a}$ . $\overrightarrow{b}$ = |$\overrightarrow{a}$| . |$\overrightarrow{b}$| ;

B. $\overrightarrow{a}$ . $\overrightarrow{b}$ = 0;

C. $\overrightarrow{a}$ . $\overrightarrow{b}$ = -1;

D. $\overrightarrow{a}$ . $\overrightarrow{b}$ = -|$\overrightarrow{a}$| . |$\overrightarrow{b}$| .

Bài 10 : Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai ?

A. $\overrightarrow{AB}$ . $\overrightarrow{AC}$ < $\overrightarrow{BA}$ . $\overrightarrow{BC}$ ;

B. $\overrightarrow{AC}$ . $\overrightarrow{CB}$ < $\overrightarrow{AC}$ . $\overrightarrow{BC}$ ;

C. $\overrightarrow{AB}$ . $\overrightarrow{BC}$ < $\overrightarrow{CA}$ . $\overrightarrow{CB}$ ;

D. $\overrightarrow{AC}$ . $\overrightarrow{BC}$ < $\overrightarrow{BC}$ . $\overrightarrow{AB}$ .

Bài 1 : Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ AB và vectơ AC:

a) cùng hướng;

b) ngược hướng.

Bài 2 : Cho ba vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ cùng phương. Chứng tỏ rằng có ít nhất hai vectơ cùng hướng trong ba vectơ đó.

Bài 3 : Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O. Hãy so sánh các vectơ AH và vectơ B'C, vectơ AB' và vectơ HC.

Bài 4 : Chứng minh rằng với hai vectơ không cùng phương a và b, ta có:

| $\overrightarrow{a}$ | - | $\overrightarrow{b}$ | ≤ |$\overrightarrow{a}$ + $\overrightarrow{b}$ | ≤ | $\overrightarrow{a}$ | + | $\overrightarrow{b}$ |

Bài 5 : Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng $\overrightarrow{OA}$ + $\overrightarrow{OB}$ + $\overrightarrow{OC}$ + $\overrightarrow{OD}$ = $\overrightarrow{0}$ .

Bài 5 : Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng

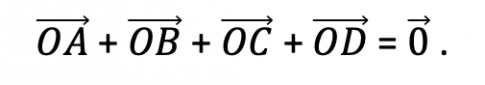
Bài 6 : Cho tam giác ABC, gọi A’ là điểm đối xứng với B qua A, gọi B’ là điểm đối xứng với C qua B, gọi C’ là điểm đối xứng với A qua C. Chứng minh rằng với một điểm O tuỳ ý, ta có: $\overrightarrow{OA}$ + $\overrightarrow{OB}$ + $\overrightarrow{OC}$ = $\overrightarrow{OA'}$ + $\overrightarrow{OB'}$ + $\overrightarrow{OC'}$

Bài 7 : Tam giác ABC là tam giác gì nếu nó thoả mãn một trong các điều kiện sau đây?

a) } $\overrightarrow{AB}$ + $\overrightarrow{AC}$ | = | $\overrightarrow{AB}$ - $\overrightarrow{AC}$ |;

b) Vectơ $\overrightarrow{AB}$ + $\overrightarrow{AC}$ vuông góc với vectơ $\overrightarrow{AB}$ + $\overrightarrow{CA}$ .

Bài 8 : Tứ giác ABCD là tứ giác gì nếu nó thoả mãn một trong các điều kiện sau đây?

a) $\overrightarrow{AC}$ - $\overrightarrow{BC}$ = $\overrightarrow{DC}$ ;

b) $\overrightarrow{DB}$ = k $\overrightarrow{DC}$ + $\overrightarrow{DA}$ .

Bài 9 : Cho tam giác ABC, trên cạnh AB lấy hai điểm M, N sao cho AM = MN = NB. Chứng minh rang hai tam giác ABC và MNC có cùng trọng tâm.

Bài 10 : Cho ba điểm O, M, N và số thực k. Lấy các điểm M' và N' sao cho $\overrightarrow{OM'}$ = k $\overrightarrow{OM}$ ; $\overrightarrow{ON'}$ = k $\overrightarrow{ON}$ . Chứng minh rằng $\overrightarrow{M'N'}$ = k $\overrightarrow{MN}$ .

Bài 11 : Cho tam giác ABC, O là điểm sao cho ba vectơ $\overrightarrow{OA}$ , $\overrightarrow{OB}$ , $\overrightarrow{OC}$ có độ dài bằng nhau và $\overrightarrow{OA}$ + $\overrightarrow{OB}$ + $\overrightarrow{OC}$ = $\overrightarrow{0}$ . Tính các góc AOB, BOC, COA. 

Bài 12 : Cho ngũ giác ABCDE. Gọi M, N, P, Q, R lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EA. Chứng minh hai tam giác EMP và NQR có cùng trọng tâm.