Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Hàm số bậc hai

Bài 1 : Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?

a) y = 3$x^{2}$ + x - √3;

b) y = $x^{2}$ + |x + 1|;

c) y = $\left\{\begin{matrix}x^{2} + 1 với x ≥ 8 &  & \\ -2x^{2} - x < 0 &  & \end{matrix}\right.$

d) y =(2$x^{2}$ +1) + 3x -1.

Bài 2 : Cho hàm số bậc hai có đồ thị là parabol có đỉnh S, đi qua các điểm A, B, C(0; – 1) được cho trong Hình 10.

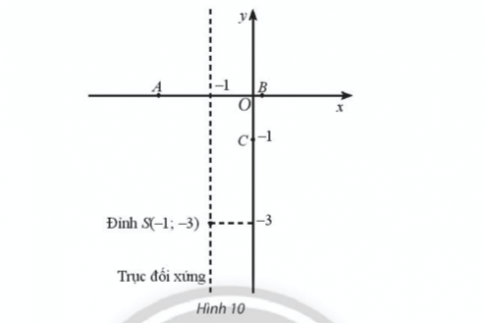
a) Vẽ đồ thị hàm số đã cho;

b) Tìm tập giá trị của hàm số và chỉ ra các khoảng biến thiên của hàm số.

Bài 3 : Tìm công thức của hàm số có đồ thị vẽ được ở Bài tập 2.

Bài 4 : Tìm công thức hàm số bậc hai biết:

a) Đồ thị hàm số đi qua 3 điểm A(1; – 3), B(0; – 2), C(2; – 10).

b) Đồ thị hàm số có trục đối xứng là đường thẳng x = 3, cắt trục tung tại điểm có tung độ bằng – 16 và một trong hai giao điểm với trục hoành có hoành độ là – 2.

Bài 5 : Tìm khoảng biến thiên và tập giá trị của các hàm số sau:

a) y = f(x) = – 2x2 – 4x + 7;

b) y = f(x) = x2 – 6x + 1.

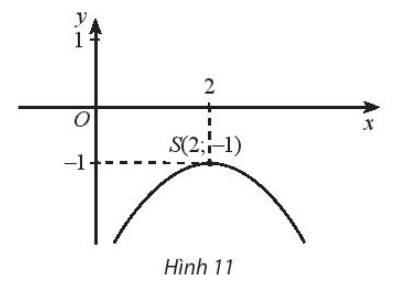
Bài 6 : Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên của hàm số biết đồ thị hàm số là một parabol có đỉnh S như Hình 11.

Bài 7 : Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu Nhật Tân là

y = f(x) = - $\frac{187}{856}$ $x^{2}$ + $\frac{8041}{856}$ x (đơn vị đo: mét).

a) Hãy tính chiều dài đoạn dây dọi sử dụng nếu khoảng cách từ chân của trụ cầu đến quả nặng là 30 cm.

b) Hãy tính khoảng cách từ chân trụ cầu đến quả nặng nếu biết chiều dài đoạn dây dọi sử dụng là 15 m.