Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài Bài tập cuối chương IV
Hướng dẫn giải bài cuối chương IV trang 80 sách bài tập toán lớp 10
Bài tập cuối chương IV trang 80 sách bài tập toán lớp 10 là một trong những bài tập quan trọng giúp học sinh ôn tập và nắm vững kiến thức trong chương. Để giải bài tập này, học sinh cần đọc kỹ từng câu hỏi, xác định yêu cầu của bài toán. Sau đó, áp dụng các kiến thức đã học để giải quyết bài toán. Đối với những bài toán phức tạp, học sinh cần suy nghĩ logic, sáng tạo để tìm ra cách giải phù hợp.
Sách bài tập "Chân trời sáng tạo" là tài liệu giáo khoa theo chương trình đổi mới của Bộ Giáo Dục, được biên soạn kỹ lưỡng và logic. Việc hướng dẫn giải chi tiết bài tập cuối chương IV giúp học sinh hiểu rõ hơn bài học, rèn luyện kỹ năng giải toán và phân tích vấn đề một cách logic.
Chúng tôi hy vọng rằng qua cách hướng dẫn cụ thể và giải chi tiết, học sinh sẽ có thêm niềm tin và sự tự tin trong việc giải toán, từ đó nâng cao khả năng học tập và hiểu bài hiệu quả.
Bài tập và hướng dẫn giải
Bài 1 : Khẳng định nào sau đây là đúng?
A. sinα = sin( 180° – α );
B. cosα = cos( 180° – α );
C. tanα = tan( 180° – α );
D. cotα = cot( 180° – α ).
Bài 2 : Trong các khẳng định sau đây, khẳng định nào sai?
A. cos45° = sin45°;
B. cos45° = sin135°;
C. cos30° = sin120°;
D. sin60° = cos120°.
Bài 3 : Bất đẳng thức nào dưới đây là đúng?
A. sin90° < sin150°;
B. sin90°15’ < sin90°30’;
C. cos90°30’ > cos100°;
D. cos150° > cos120°.
Bài 4 : Trong các đẳng thức sau đây, đẳng thức nào là đúng?
A. sin150° = $\frac{-√3}{2}$;
B. cos150° = $\frac{√3}{2}$;
C. tan150° = $\frac{-1}{√3}$;
D. cot150° = √3.
Bài 5 : Cho tam giác ABC có BC = a, AC = b, AB = c. Mệnh đề nào sau đây đúng?
A. Nếu b2 + c2 – a2 > 0 thì góc A nhọn;
B. Nếu b2 + c2 – a2 > 0 thì góc A tù;
C. Nếu b2 + c2 – a2 < 0 thì góc A nhọn;
D. Nếu b2 + c2 – a2 < 0 thì góc A vuông.
Bài 6 : Cho tam giác ABC có AB = 4 cm, BC = 7 cm, CA = 9 cm. Giá trị cosA là:
A. $\frac{2}{3}$ ;
B. $\frac{1}{3}$ ;
C. $\frac{-2}{3}$ ;
D. $\frac{1}{2}$.
Bài 7 : Cho tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64cm2. Giá trị sinA là:
A. $\frac{√3}{2}$ ;
B. $\frac{3}{8}$;
C. $\frac{4}{5}$;
D. $\frac{8}{9}$.
Bài 8 : Cho tam giác ABC vuông cân tại A có AB = AC = 30 cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC là:
A. 50 cm2;
B. 502">√2 cm2;
C. 75 cm2;
D. 15105">√105 cm2.
Bài 9 : Tam giác ABC có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
A. 2S;
B. 3S;
C. 4S;
D. 6S.
Bài 10 : Cho góc xOy = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
A. 1,5;
B. 3">√3;
C. 22">2√2;
D. 2.
Bài 1 : Cho tam giác ABC với ba cạnh a, b, c. Chứng minh rằng:
$\frac{cosA}{a}$ + $\frac{cosB}{b}$ + $\frac{cosC}{c}$ = $\frac{a2 + b2 + c2}{2abc}$ .
Bài 2 : Cho tam giác ABC. Biết a = 24; b = 36; góc C = 52°. Tính cạnh c và hai góc A, góc B
Bài 3 : Hai chiếc tàu thủy P và Q cách nhau 50 m. Từ P và Q thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới các góc
BPA = 40° và góc BQA = 52°. Tính chiều cao của tháp hải đăng đó.
Bài 4 : Cho tam giác ABC có góc A = 99°, b = 6, c = 10. Tính:
a) Diện tích tam giác ABC;
b) Bán kính đường tròn ngoại tiếp và bán kính đường tròn nội tiếp tam giác ABC.
Bài 5 : Hai máy bay rời một sân bay cùng một lúc. Một chiếc máy bay với vận tốc 800 km/h theo hướng lệch so với hướng bắc 15° về phía tây. Chiếc còn lại bay theo hướng lệch so với hướng nam 45° về phía tây với vận tốc 600 km/h ( Hình 1). Hỏi hai máy bay đó cách nhau bao xa sau 3 giờ?

Bài 6 : Cho tam giác ABC không vuông. Chứng minh rằng:
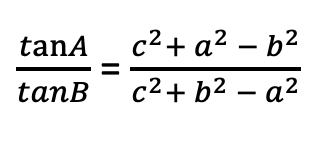
Bài 7 : Một tháp viễn thông cao 42 m được dựng thẳng đứng trên một sườn dốc 34° so với phương ngang. Từ đỉnh tháp người ta neo một sợi cáp xuống một điểm trên sườn dốc cách chân tháp 33 m như Hình 2. Tính chiều dài của sợi dây cáp đó.