Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài Bài tập cuối chương III

Bài 1 : Một hàm số có thể được cho bằng:

A. Bảng giá trị của hàm số;

B. Đồ thị của hàm số;

C. Công thức của hàm số;

D. Tất cả đều đúng.

Bài 2 : Cho hàm số y = f(x) = 2(x + 1)(x – 3) + 2x – 6. Giá trị của hàm số khi x = 3 là:

A. 8;

B. 0;

C. – 6;

D. 3.

Bài 3 : Hàm số y = f(x) = y = f(x) = $\sqrt{x - 1}$ + $\frac{1}{x^{2} - 9}$ có tập xác định D là :

A. D = [1; + ∞);

B. D = ℝ \ {– 3; 3};

C. D = [1; + ∞) \ {3};

D. D = [3; + ∞).

Bài 4 : Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?

A. y = f(x) = $\sqrt{3}$ 3">$x^{2}$ + x – 4;

B. y = f(x) = $x^{2}$ + $\frac{1}{x}$ – 5;

C. y = f(x) = – 2x(x – 1);

D. y = f(x) = 2($x^{2}$ + 1) + 3x – 1.

Bài 5 : Tập giá trị của hàm số y = f(x) = – 2$x^{2}$  + $\sqrt{2}$x + 1 là :

A. T = ($\frac{-5}{4}$ ; +∞);

B. T = [$\frac{-5}{4}$ ; +∞);

C. T = (−∞ ; $\frac{5}{4}$); 

D. T = (−∞ ; $\frac{5}{4}$].

Bài 6 : Hàm số y = f(x) = –(x + 2)(x – 4) đồng biến trên khoảng:

A. (– ∞; – 1);

B. (1; + ∞);

C. (– ∞; 1);

D. (– 1; + ∞).

Bài 7 : Hàm số y = f(x) = (x + 2)(x – 2) có:

A. Giá trị nhỏ nhất là 4;

B. Giá trị lớn nhất là 4;

C. Giá trị lớn nhất là – 4;

D. Giá trị nhỏ nhất là – 4.

Bài 8 : Để hàm số y = f(x) = (m – 2)(x + 5)2 + (m2 – 4) |x – 7| + 3 là một hàm số bậc hai thì giá trị của m là:

A. 2;

B. 2 hay – 2;

C. – 2;

D. 4.

Bài 9 : Đồ thị hàm số y = f(x) = –x2 + 4(5m + 1)x + (3 – 2m) có trục đối xứng là đường thẳng x = – 2 khi m có giá trị là:

A. – 3;

B. −25">−25−25;

C. 32">3232;

D. −15">−15−15.

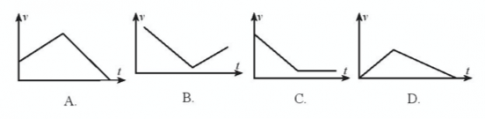
Bài 10 : Một viên bi được thả không vận tốc đầu và lăn trên máng nghiêng như Hình 1.

Đồ thị nào sau đây phù hợp với sự thay đổi vận tốc của viên bi theo thời gian?

Bài 1 : Ta có bảng giá trị của hàm cầu đối với sản phẩm A theo đơn giá của sản phẩm A như sau:

a) Giả sử hàm cầu là một hàm số bậc hai theo đơn giá x, hãy viết công thức của hàm này, biết rằng c = 392.

b) Chứng tỏ rằng hàm số này có thể viết thành dạng y = f(x) = a(b – x)2.

c) Giả sử hàm cầu này lấy mọi giá trị trên đoạn [0; 100], hãy tính lượng cầu khi đơn giá sản phẩm A là 30, 50, 100.

d) Cùng giả thiết với câu c, nếu lượng cầu là 150 sản phẩm thì đơn giá sản phẩm A là khoảng bao nhiêu (đơn vị: nghìn đồng)?  

Bài 2 : Khi một vật từ vị trí y0 được ném xiên lên cao theo góc α (so với phương ngang) với vận tốc ban đầu v0 thì phương trình chuyển động của vật này là:

a) Vật bị ném xiên như vậy có chuyển động theo đường xiên hay không? Tại sao?

b) Giả sử góc ném có số đo là 45°, vận tốc ban đầu của vật là 3 m/s và vật được ném xiên từ độ cao 1 m so với mặt đất, hãy viết phương trình chuyển động của vật.

c) Một vận động viên ném lao đã lập kỉ lục với độ xa 90 m. Biết người này ném lao từ độ cao 0,9 m và góc ném là khoảng 45°. Hỏi vận tốc đầu của lao khi được ném đi là bao nhiêu?

(Lưu ý: Lấy giá trị g = 10 m/s2 cho gia tốc trọng trường và làm tròn kết quả đến 2 chữ số thập phân).