Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo Bài tập cuối chương IX

A. TRẮC NGHIỆM

Bài tập 1. Cho hai vectơ $\overrightarrow{a} $ = (4; 3) và $\overrightarrow{b}$ = (1; 7). Góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là:

A. $90^{o}$;          B. $60^{o}$;          C. $45^{o}$;          D. $30^{o}$.

Bài tập 2. Cho hai điểm M = (1; -2) và N = (-3; 4). Khoảng cách giữa hai điểm M và N là:

A. 4;          B. 6;         C. $3\sqrt{6}$;         D. $2\sqrt{13}$.

Bài tập 3. Tam giác ABC có A = (-1; 1), B = (1; 3) và C = (1; -1). Trong các phát biểu sau đây, phát biểu nào đúng?

A. ABC là tam giác có ba cạnh bằng nhau;

B. ABC là tam giác có ba góc đều nhọn;

C. ABC là tam giác cân tại B (có BA = BC);

D. ABC là tam giác vuông cân tại A.

Bài tập 4. Cho phương trình tham số của đường thẳng d: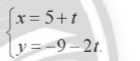

Trong các phương trình sau, phương trình nào là phương trình tổng quát của (d)?

A. 2x + y - 1 = 0;          B. 2x + 3y + 1 = 0;

C. x + 2y + 2 = 0;          D. x + 2y - 2 = 0.

Bài tập 5. Đường thẳng đi qua điểm M(1; 0) và song song với đường thẳng d: 4x + 2y + 1 = 0 có phương trình tổng quát là:

A. 4x + 2y + 3 = 0;          B. 2x + y + 4 = 0;

C. 2x + y - 2 = 0;             D. x - 2y + 3 - 0.

Bài tập 6. Bán kính của đường tròn tâm I(0; -2) và tiếp xúc với đường thẳng $\Delta$: 3x - 4y - 23 = 0 là:

A. 15;          B. 5;          C. $\frac{3}{5}$;          D. 3.

Bài tập 7. Cho đường tròn (C): $x^{2} + y^{2} + 2x + 4y - 20 = 0$. Trong các mệnh đề sau đây, phát biểu nào sai?

A. (C) có tâm I(1; 2);               B. (C) có bán kính R = 5;

C. (C) đi qua điểm M(2; 2);     D. (C) không đi qua điểm A(1; 1).

Bài tập 8. Phương trình tiếp tuyến tại điểm M(3; 4) với đường tròn (C): $x^{2} + y^{2} - 2x - 4y + 3 = 0$ là:

A. x + y - 7 = 0;          B. x + y + 7 = 0;

C. x - y - 7 = 0;           D. x + y - 3 = 0.

Bài tập 9. Phương trình chính tắc của elip có hai đỉnh là (-3; 0), (3; 0) và hai tiêu điểm là (-1; 0), (1; 0) là:

A. $\frac{x^{2}}{9} + \frac{y^{2}}{1} = 1$;        B. $\frac{x^{2}}{8} + \frac{y^{2}}{9} = 1$;

C. $\frac{x^{2}}{9} + \frac{y^{2}}{8} = 1$;        D. $\frac{x^{2}}{1} + \frac{y^{2}}{9} = 1$.

Bài tập 10. Phương trình chính tắc của hypebol có hai đỉnh là (-4; 0), (4; 0) và hai tiêu điểm là (-5, 0), (5; 0) là:

A. $\frac{x^{2}}{16} - \frac{y^{2}}{25} = 1$;          B. $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$;

C. $\frac{x^{2}}{100} - \frac{y^{2}}{36} = 1$;        D. $\frac{x^{2}}{64} - \frac{y^{2}}{36} = 1$;

Bài tập 11. Phương trình chính tắc của parabol có tiêu điểm (2; 0) là:

A. $y^{2} = 8x$;          B. $y^{2} = 4x$;          C. $y^{2} = 2x$;          D. $y = 2x^{2}$.

Bài tập 12. Elip với độ dài hai trục là 20 và 12 có phương trình chính tắc là:

A. $\frac{x^{2}}{40} + \frac{y^{2}}{12} = 1$;            B. $\frac{x^{2}}{1600} + \frac{y^{2}}{144} = 1$;

C. $\frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$;          D. $\frac{x^{2}}{64} + \frac{y^{2}}{36} = 1$.

B. TỰ LUẬN

Bài tập 1. Trong mặt phẳng Oxy cho ba điểm A(2; 2), B(1; 3), C(-1; 1).

a) Chứng minh OABC là một hình chữ nhật;

b) Tìm toạ độ tâm I của hình chữ nhật OABC.

Bài tập 2. Tìm góc giữa hai đường thẳng $d_{1}$ và $d_{2}$.

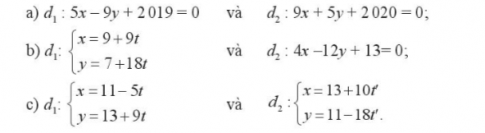
Bài tập 3. Cho tam giác ABC với toạ độ ba đỉnh là 4(1; 1), B(3; 1); C(1; 3). Tính độ dài đường cao AH.

Bài tập 4. Tính bán kính của đường tròn tâm J(1; 0) và tiếp xúc với đường thẳng d: 8x - 6y + 22 = 0.

Bài tập 5. Tính khoảng cách giữa hai đường thẳng:

$\Delta$: ax + by + c = 0 và $\Delta'$: ax+ by + d = 0 (biết $\Delta // \Delta'$).

Bài tập 6. Tìm tâm và bán kính của các đường tròn có phương trình:

a) $(x + 1)^{2} + (y + 2)^{2} = 225$;

b) $x^{2} + (y - 7)^{2} = 5$;

c) $x^{2} + y^{2} = 10x =24y = 0$.

Bài tập 7. Lập phương trình đường tròn trong các trường hợp sau:

a) Có tâm I(2; 2) và bán kính bằng 7;

b) Có tâm J(0; -3) và đi qua điểm M(-2; -7);

c) Đi qua hai điểm A(2; 2), B(6; 2) và có tâm nằm trên đường thẳng x - y = 0;

d) Đi qua gốc toạ độ và cắt hai trục toạ độ tại các điểm có hoành độ là 8, tung độ là 6.

Bài tập 8. Viết phương trình tiếp tuyến với đường tròn (C): $(x - 1)^{2} + (y - 1)^{2} = 25$ tại điểm A(4; 5).

Bài tập 9. Gọi tên các đường conic sau:

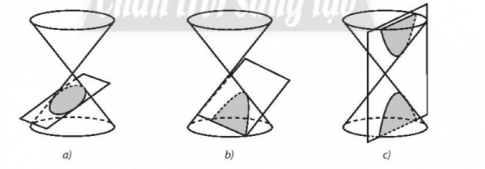
Bài tập 10. Tìn tọa độ các tiêu điểm, tọa độ các đỉnh, độ đài trục lớn và trục nhỏ của các elip sau:

a) $\frac{x^{2}}{169} + \frac{y^{2}}{25} = 1$;          b) $x^{2} + 4y^{2} = 1$.

Bài tập 11. Viết phương trình chính tắc của elip thỏa mãn các điều kiện sau:

a) Độ dài trục lớn 26, độ đài trục nhỏ 10;

b) Độ dài trục lớn 10, tiêu cự 6.

Bài tập 12. Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:

a) $\frac{x^{2}}{25} - \frac{y^{2}}{144} = 1$;          b) $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$.

Bài tập 13. Viết phương trình chính tắc của hypebol thỏa mãn các điêu kiện sau:

a) Đỉnh (-6, 0) và (6; 0); tiêu điểm (-10; 0) và (10; 0);

b) Độ dài trục thực là 10, độ đài trục ảo là 20.

Bài tập 14. Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:

a) $y^{2} = 4x$;          b) $y^{2} = 2x$;          c) $y^{2} = -6x$.

Bài tập 15. Viết phương trình chính tắc của parabol thỏa mãn các điều kiện:

a) Tiêu điểm (8; 0);

b) Khoảng cách từ tiêu điểm đến đường chuẩn bằng 4.

Bài tập 16. Một nhà mái vòm có mặt cắt hình nửa elip cao 6 m rộng 16 m.

a) Hãy chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên;

b) Tính khoảng cách thẳng đứng từ một điểm cách chân vách 4 m lên đến mái vòm.

Bài tập 17. Cho biết Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là elip (E) với Trái Đất là mội tiêu điểm. Cho biết độ đài hai trục của (E) là 768 800 km và 767 619 km. Viết phương trình chính tắc của elip (E).

Bài tập 18. Gương phản chiếu của một đèn pha có mặt cắt là một parabol (P) với tim bóng đèn đặt ở tiêu điểm F. Chiều rộng giữa hai mép gương là 50 cm, chiều sâu của gương là 40 cm. Viết phương trình chính tắc của (P).

Bài tập 19. Màn hình của rađa tại trạm điều khiển không lưu được thiết lập hệ toạ độ Oxy với vị trí trạm có tọa độ O(0; 0) và rađa có bán kính hoạt động là 600 km. Một máy bay khởi hành từ sân bay lúc 8 giờ. Cho biết sau t giờ máy bay có toạ độ:

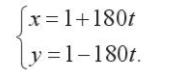
a) Tìm toạ độ máy bay lúc 9 giờ;

b) Tính khoảng cách giữa máy bay và trạm điều khiển không lưu;

c) Lúc mấy giờ máy bay ra khỏi tầm hoạt động của rađa?