Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 4 Ba đường conic trong mặt phẳng tọa độ
Hướng dẫn giải bài 4 Ba đường conic trong mặt phẳng tọa độ trang 71 sách bài tập (SBT) toán lớp 10 tập 2
Trong bài này, chúng ta sẽ tìm hiểu về ba đường conic trong mặt phẳng tọa độ. Ba đường conic bao gồm elip, parabol và hyperbol. Để giải bài tập này, đầu tiên chúng ta cần xác định loại conic mà đường đã cho thuộc về. Sau đó, áp dụng các kiến thức về phương trình đường conic để tìm ra các thông tin cần thiết như tâm, trục lớn, trục ngắn, focus, directrix, và các điểm nổi bật khác của đường conic.
Sau khi đã xác định được các thông tin trên, chúng ta có thể dễ dàng vẽ đồ thị của đường conic và hiểu rõ hơn về hình dạng của nó. Việc này giúp chúng ta áp dụng kiến thức đã học vào thực tế và nắm vững bài học.
Với cách hướng dẫn chi tiết và giải thích rõ ràng trong sách bài tập (SBT) toán lớp 10, hy vọng rằng học sinh sẽ có thể giải bài tập một cách dễ dàng và hiểu bài học tốt hơn.
Bài tập và hướng dẫn giải
Bài tập 1. Viết phương trình chính tắc của:
a) Elip có trục lớn bằng 12 và trục nhỏ bằng 8;
b) Hypebol có tiêu cự 2c = 18 và độ dài trục thực 2a = 14;
c) Parabol có tiêu điểm F(5; 0).
Bài tập 2. Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ các tiêu điểm của chúng.
a) $(C_{1}): 7x^{2} + 13y^{2} = 1$; b) $(C_{2}): 25x^{2} - 9y^{2} = 225$; c)$(C_{3}): x = 2y^{2}$
Bài tập 3. Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 1 m và trục nhỏ là 0,6 m từ một tấm ván ép hình chữ nhật có kích thước 1 m x 0,6 m, người ta vẽ hình elip đó lên tấm ván ép như hướng dẫn sau:
Chuẩn bị:
- Hai cái đinh, một vòng dây kín không đàn hồi, bút chì. `
Thực hiện:
- Xác định vị trí (hai tiêu điểm của elip) và ghim hai cái đinh lên hai điểm đó trên tấm ván.
- Quàng vòng dây qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm AM rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà ta gọi la đường elip. (Xem minh họa Hình 10).
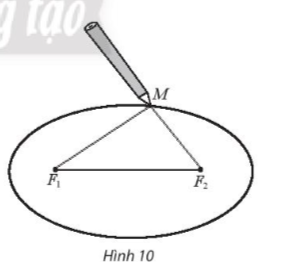
Phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài là bao nhiêu?
Bài tập 4. Thang leo gợn sóng cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 100 cm và khoảng cách giữa hai chân là 240 cm.
a) Hãy chọn hệ tọa độ thích hợp và viết phương trình chính tắc của elip nói trên.
b) Tính khoảng cách thẳng đứng từ một điểm cách chân khung 20 cm lên đến khung thép.
Bài tập 5. Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình $\frac{x^{2}}{30^{2}} - \frac{y^{2}}{50^{2}} = 1$. Biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng $\frac{1}{2}$ khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính đáy của tháp.
Bài tập 6. Một cái cầu có dây cáp treo hình parabol, cầu dài 120 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 48 m, thanh ngắn nhất là 8 m (Hình 12). Tính chiều dài của thanh cách điểm giữa cầu 20 m.