Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 1 Dấu của tam thức bậc hai
Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo: Bài 1 Dấu của tam thức bậc hai
Trong sách bài tập toán lớp 10 tập 2, bài 1 Dấu của tam thức bậc hai được hướng dẫn giải chi tiết trên trang 5. Đây là một phần trong bộ sách "Chân trời sáng tạo" được biên soạn theo chương trình mới của Bộ giáo dục. Mục tiêu của sách là giảng dạy học sinh cách giải các bài toán một cách cụ thể và rõ ràng.
Hướng dẫn giải bài 1 Dấu của tam thức bậc hai trang 5 sách bài tập toán lớp 10 tập 2 làm cho học sinh dễ nắm bài học hơn. Bằng cách giải thích cụ thể và chi tiết, việc học toán trở nên thú vị và dễ dàng hơn.
Qua cách hướng dẫn này, việc giải bài toán tam thức bậc hai sẽ trở nên hiệu quả hơn và học sinh sẽ có khả năng áp dụng kiến thức vào thực tế một cách chính xác.
Bài tập và hướng dẫn giải
Bài tập 1. Tính biệt thức và nghiệm (nếu có) của các tam thức bậc hai sau. Xác định dấu của chúng tại x = -2.
a) f(x) = $-2x^{2}$ + 3x - 4;
b) g(x) = $2x^{2}$ + 8x + 8;
c) h(x) = $3x^{2}$ + 7x - 10.
Bài tập 2. Tìm các giá trị của tham số m để:
a) f(x) = $(2m - 8)x^{2} + 2mx + 1$ là một tam thức bậc hai;
b) f(x) = $(2m + 3)x^{2} + 3x - 4m^{2}$ là một tam thức bậc hai có x = 3 là một nghiệm;
c) f(x) = $2x^{2} + mx - 3$ dương tại x = 2.
Bài tập 3. Tìm các giá trị của tham số m để:
a) f(x) = $(m^{2} + 9)x^{2} + (m + 6)x +1$ là một tam thức bậc hai có một nghiệm duy nhất;
b) f(x) = $(m - 1)x^{2} + 3x + 1$ là mội tam thức bậc hai có hai nghiệm phân biệt;
c) f(x) = $mx^{2} + (m + 2)x + 1$ là một tam thức bậc hai vô nghiệm.
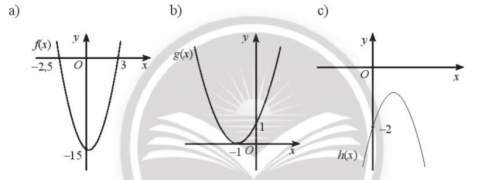
Bài tập 4. Dựa vào đồ thị của các hàm số bậc hai được cho trong hình dưới đây, xét dấu của tam thức bậc hai tương ứng:
Bài tập 5. Xét dấu của các tam thức bậc hai sau:
a) f(x) = $x^{2} - 5x + 4$; b) f(x) = $-\frac{1}{3}x^{2} + 2x - 3$;
c) f(x) = $3x^{2} + 6x + 4$; d) f(x) = $-2x^{2} + 3x + 5$;
e) f(x) = $-6x^{2} + 3x - 1$; g) f(x) = $4x^{2} + 12x + 9$.
Bài tập 6. Tìm các giá trị của tham số m để:
a) f(x) = $(m + 1)x^{2} + 5x + 2$ là tam thức bậc hai không đổi dấu trên $\mathbb{R}$;
b) f(x) = $mx^{2} - 7x + 4$ là tam thức bậc hai âm với mọi x $\in \mathbb{R}$;
c) f(x) = $3x^{2} - 4x +(3m + 1)$ là tam thức bậc hai dương với mọi x $\in \mathbb{R}$;
d) f(x) = $(m^{2} + 1)z^{2} - 3mx + 1$ là tam thức bậc hai âm với mọi x $\in \mathbb{R}$.
Bài tập 7. Chứng minh rằng:
a) $2x^{2} + \sqrt{3}x + 1 > 0$ với mọi x $\in \mathbb{R}$;
b) $x^{2} + x + \frac{1}{4} \geq 0$ với mọi x $\in \mathbb{R}$;
c) $-x^{2} < -2x + 3$ với mọi x $\in \mathbb{R}$.
Bài tập 8. Xác định giá trị của các hệ số a, b, c và xét dấu của tam thức bậc hai f(x)= $ax^{2} + bx + c$ trong mỗi trường hợp sau:
a) Đồ thị của hàm số y = f(x) đi qua ba điểm có toạ độ là (-1; -4), (0; 3) và(1; -14);
b) Đồ thị của hàm số y = f(x) đi qua ba điểm có toạ độ là (0; -2), (2; 6) và (3; 13);
c) f(-5) = 33, f(0) = 3 và f(2) = 19.





