Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Đường thẳng trong mặt phẳng tọa độ
Hướng dẫn giải bài 2 Đường thẳng trong mặt phẳng tọa độ
Để giải bài 2 về đường thẳng trong mặt phẳng tọa độ trang 60 sách bài tập (SBT) toán lớp 10 tập 2, đầu tiên cần đọc đề bài một cách cẩn thận để hiểu rõ yêu cầu. Tiếp theo, xác định tọa độ của các điểm có liên quan như điểm qua đường thẳng, điểm cắt với trục tọa độ, v.v.
Sau khi đã xác định các tọa độ, sử dụng công thức tính khoảng cách giữa 2 điểm, công thức cấp số nhân, hay công thức nào khác phù hợp để giải bài toán. Đảm bảo tính chính xác và logic trong quá trình giải.
Đây là sách bài tập "Chân trời sáng tạo" được biên soạn theo chương trình đổi mới của Bộ giáo dục, hướng dẫn cụ thể và giải chi tiết giúp học sinh nắm vững kiến thức. Hy vọng học sinh sẽ học tốt hơn và hiểu rõ hơn về bài toán đường thẳng trong mặt phẳng tọa độ sau khi tham khảo sách này.
Bài tập và hướng dẫn giải
Các bài toán san đây được xét tong mặt phẳng Oxy.
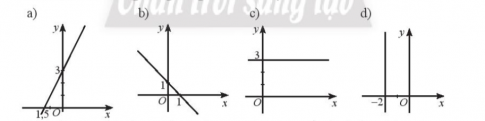
Bài tập 1. Tìm các giá trị của tham sô a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được các đường thẳng trong hình dưới đây.
Bài tập 2. Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm M(2; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (4; 7);
b) d đi qua điểm M(0; 1) và có vectơ pháp tuyến là $\overrightarrow{n}$ (-5; 3);
c) d đi qua A(-2; -3) và có hệ số góc k = 3;
d) d đi qua hai điểm P(1; 1) và Q(3; 4).
Bài tập 3. Cho tam giác ABC, biết A(1; 4), B(0; 1) và C(4; 3).
a) Lập phương trình tổng quát của đường thẳng BC.
b) Lập phương trình tham số của đường trung tuyên AM.
c) Lập phương trình tổng quát của đường cao AH.
Bài tập 4. Lập phương trình tổng quát của đường thẳng $\Delta$ trong mỗi trường hợp sau:
a) $\Delta$ đi qua M(3; 3) và song song với đường thẳng x + 2y - 2 022 = 0;
b) $\Delta$ đi qua N(2; -1) và vuông góc với đường thẳng 3x + 2y + 99 = 0.
Bài tập 5. Xét vị trí tương đối của các cặp đường thẳng $d_{1}$ và $d_{2}$ sau đây:
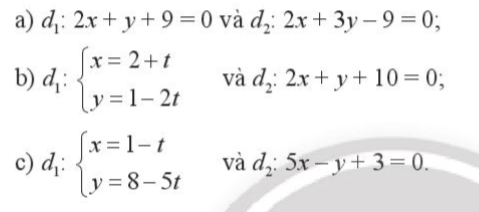
Bài tập 6. Cho đường thẳng d có phương trình tham số: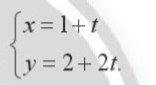
Tìm giao điểm của d với đường thẳng $\Delta$ x + y - 2 = 0.
Bài tập 7. Tìm số đo của góc giữa hai đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau:
a) $d_{1}$: 5x - 3y + 1 = 0 và $d_{2}$: 10x - 6y - 7 = 0;
b) $d_{1}$: 7x - 3y + 7 = 0 và $d_{2}$: 3x + 7y - 10 = 0;
c) $d_{1}$: 2x - 4y + 9 = 0 và $d_{2}$: 6x - 2y - 2 023 = 0.
Bài tập 8. Tính khoảng cách từ điềm M đến đường thẳng $\Delta$ trong các trường hợp sau:
a) M(2; 3) và $\Delta$: 8x - 6y + 7 = 0; b) M(0; 1) và $\Delta$: 4x + 9y - 20 = 0;
c) M(1; 1) và $\Delta$: 3y - 5 = 0; d) M(4; 9) và $\Delta$: x - 25 = 0.
Bài tập 9. Tìm c để đường thẳng $\Delta$: 4x - 3y + c = 0 tiếp xúc với đường tròn (C) có tâm J(1; 2) và bán kính R = 3.
Bài tập 10. Tính khoảng cách giữa hai đường thẳng:
$\Delta$: 6x + 8y - 11 = 0 và $\Delta'$: 6x + 8y - 1 = 0.
Bài tập 11. Một trạm viễn thông S có tọa độ (5, 1). Một người đang ngồi trên chiếc xe khách chạy trên đoạn cao tốc có đang một đường thẳng $\Delta$ có phương trình 12x + 5y - = 0. Tính khoảng cách ngắn nhất giữa người đó và trạm viễn thông S. Biết rằng mỗi đơn vị độ đài tương ứng với 1 km.