Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Giải bài tập bất phương tình bậc hai một ẩn
Hướng dẫn giải bài 2 Giải bất phương tình bậc hai một ẩn
Trong sách bài tập (SBT) toán lớp 10 chân trời sáng tạo, bài tập 2 là bài toán giải bất phương trình bậc hai với một ẩn được trình bày trên trang 10. Đây là một phần trong bộ sách "Chân trời sáng tạo" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Mục tiêu của việc hướng dẫn giải bài tập này là giúp học sinh hiểu bài học một cách cụ thể và chi tiết hơn.
Với cách hướng dẫn dễ hiểu và giải thích chi tiết, việc này giúp học sinh nắm vững kiến thức và kỹ năng giải bài toán bất phương trình bậc hai một cách chính xác. Hy vọng rằng thông qua bài tập này, học sinh sẽ tự tin hơn trong việc giải các bài toán phức tạp hơn trong tương lai.
Bài tập và hướng dẫn giải
Bài tập 1. x = 2 là một nghiệm của bất phương trình nào sau đây?
a) $x^{2} - 3x + 1 > 0$;
b) $-4x^{2} - 3x + 5 \leq 0$;
c) $2x^{2} - 5x + 2 \leq 0$.
Bài tập 2. Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng.
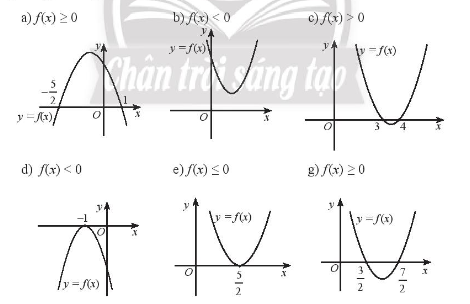
Bài tập 3. Giải các bất phương trình bậc hai sau:
a) $-9x^{2} + 15x + 4 \leq 0$; b) $6x^{2} - 13x - 33 < 0$;
c) $7x^{2} - 36x + 5 \leq 0$; d) $-9x^{2} + 6x - 1 \geq 0$;
e) $49x^{2} + 56x + 16 > 0$; g) $-2x^{2} + 3x - 2 \leq 0$.
Bài tập 4. Giải các bất phương trình bậc hai sau:
a) $x^{2} - 3x < 4$; b) $0< 2x^{2} - 11x - 6$;
c) $-2(2x + 3)x^{2} + 4x + 30 \leq 0$; d) $-3(x^{2} -4x - 1) \leq x^{2} - 8x + 28$;
e) $2(x - 1)x^{2} \geq 3x^{2} + 6x + 27$; g) $2(x + 1)^{2} + 9(-x + 2) < 0$.
Bài tập 5. Tìm tập xác định của các hàm số sau:
a) y = $\sqrt{15x^{2} + 8x - 12}$; b) $\frac{x - 1}{\sqrt{-11x^{2} + 30x - 16}}$;
c) $\frac{1}{x - 2} - \sqrt{-x^{2} + 5x - 6}$; d) $\frac{1}{\sqrt{2x + 1}} - \sqrt{6x^{2} - 5x - 21}$.
Bài tập 6. Tìm giá trị của tham số m để:
a) x = 3 là một nghiệm của bất phương trình $(m^{2} - 1)x^{2} + 2mx - 15 \leq 0$;
b) x = -1 là một nghiệm của bất phương trình $mx^{2} - 2x + 1 > 0$;
c) x = $\frac{5}{2}$ là một nghiệm của bất phương trình $4x^{2} =2mx - 5m \leq 0$;
d) x = -2 là một nghiệm của bất phương trình $(2m - 3)x^{2} - (m^{2} + 1)x \geq 0$;
e) x = m + 1 là một nghiệm của bất phương trình $2x^{2} + 2mx - m^{2} -2 < 0$.
Bài tập 7. Với giá trị nào của tham số m thì:
a) Phương trình $4x^{2} + 2 (m - 2)x + m^{2}$ có nghiệm;
b) Phương trình $(m + 1)x^{2} + 2mx - 4 = 0$ có hai nghiệm phân biệt;
c) Phương trình $mx^{2} + (m + 1)x + 3m + 10 = 0$ vô nghiệm;
d) Bất phương trình $2x^{2} + (m + 2)x + (2m _ 4) > 0$ có tập nghiệm là $\mathbb{R}$;
e) Bất phương trình $-3x^{2} + 2mx + m^{2} \geq 0$ có lập nghiệm là $\mathbb{R}$.
Bài tập 8. Lợi nhận thu được từ việc sản xuất và bán x sản phẩm thủ công của một cửa hàng là:
I(x) = $-0,1x^{2} + 235x - 70 000$,
với I được tính bằng nghìn đồng. Với số lượng sản phẩm bán ra là bao nhiêu thì cửa hàng có lãi?
Bài tập 9. Một quả bóng được ném thẳng lên từ độ cao $h_{0}$ (m) với vận tốc $v_{0}$ (m/s). Độ cao của bóng so với mặt đất (tính bằng mét) sau t (s) được cho bởi hàm số $h_{t} = -\frac{1}{2}gt^{2} + v_{0}t + h_{0}$ với g = 10 m/$s^{2}$ là gia tốc trọng trường.
a) Tính $h_{0}$ và $v_{0}$ biết độ cao của quả bóng sau 0,5 giây và 1 giây lần lượt là 4,75 mm và 5m.
b) Quả bóng có thể đạt được độ cao trên 4 m không? Nếu có thì trong thời gian bao lâu?
c) Cũng ném từ độ cao $h_{0}$ như trên, nếu muốn độ cao của bóng sau 1 giây trong khoảng từ 2 m đến 3 m thì vận tốc ném bóng $v_{0}$ cần là bao nhiêu?
Lưu ý: Đáp số làm tròn đến hàng phần trăm
Bài tập 10. Từ độ cao $y_{0}$ mét, một quả bỏng được ném lên xiên một góc $\alpha$ so với phương ngang với vận tốc đầu và có phương trình chuyển động
y = $\frac{-g}{2v_{0}^{2}cos^{2}\alpha}x^{2} + (tan\alpha) + y_{0}$ với g = 10 m/$s^{2}$
a) Viết phương trình chuyển động của quả bóng nếu $\alpha = 30^{o}$, $y_{0}$ = 2 m và $v_{0}$ = 7 m/s.
b) Để ném được quả bóng qua bức tường cao 2,5 m thì người ném phải đứng cách tường bao xa?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Bài tập 11. Một hình chữ nhật có chu vi bằng 20 cm. Để diện tích hình chữ nhật lớn hơn hoặc bằng 15 $cm^{2}$ thì chiều rộng của hình chữ nhật nằm trong khoảng bao nhiêu?
Bài tập 12. Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m.
a) Chọn trục hòanh là đường thẳng nối hai chân cổng, gốc tọa độ tại một chân cổng, chân cổng còn lại có hoành độ dương, đơn vị là 1 m. Hãy viết phương trình của vòm cổng.
b) Người ta cần chuyển mội thùng hàng hình hộp chữ nhật với chiều cao 3 m. Chiều rộng của thùng hàng tối đa là bao nhiêu để thùng có thể chuyển lọt qua được cổng?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.





