Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Xác suất của biến cố
Hướng dẫn giải bài 2 Xác suất của biến cố trang 97 sách bài tập (SBT) toán lớp 10 tập 2
Trong bài toán xác suất này, chúng ta cần xác định xác suất của biến cố nào đó. Để giải bài toán này, ta cần làm những bước sau:
1. Xác định số cách xảy ra của biến cố cần tính xác suất.
2. Xác định tổng số trường hợp có thể xảy ra.
3. Tính xác suất bằng cách chia số cách xảy ra của biến cố cho tổng số trường hợp có thể xảy ra.
Qua việc thực hiện các bước trên, chắc chắn bạn sẽ có thể giải bài toán xác suất một cách dễ dàng và chính xác. Chúc các bạn học tốt và thành công!
Bài tập và hướng dẫn giải
Bài tập 1. Gieo một con xúc xắc 4 mặt cân đối và đồng chất ba lần. Tính xác suất của các biến cố:
a) “Tổng các số xuất hiện ở đỉnh phía trên của con xúc xắc trong ba lần gieo lớn hơn 2”;
b) “Có đúng một lần số xuất hiện ở đỉnh phía trên của con xúc xắc là 2”.
Bài tập 2. Tung một đồng xu cân đối và đồng chất bốn lần. Tính xác suất của các biến cố:
a) “Cả bốn lần đều xuất hiện mặt giống nhau”;
b) “Có đúng một lần xuât hiện mặt sấp, ba lần xuất hiện mặt ngửa”.
Bài tập 3. Chi có 1 cái ô xanh, 1 cái ô trắng; 1 cái mũ xanh, 1 cái mũ trắng, 1 cái mũ đen; 1 đôi giày đen, 1 đôi giày trắng. Chi chọn ngẫu nhiên 1 cái ô, 1 cái mũ và 1 đôi giày để đến trường.
a) Hãy vẽ sơ đồ cây mô tả các kết quả có thể xảy ra.
b) Tính xác suất của biến cố "Chỉ có 1 trong 3 thứ đồ Chi chọn có màu trắng”.
Bài tập 4. Chọn ngẫu nhiên 10 số tự nhiên từ dãy các số tự nhiên từ 1 đến 100. Xác định biến cố đôi của các biến cố sau:
A: “Có ít nhất 3 số lẻ trong 10 số được chọn”;
B: “Tất cả 10 số được chọn đều là số chẵn”;
C: “Có không quá 5 số chẵn trong 10 số được chọn”.
Bài tập 5. Trên tường có một đĩa hình tròn có cấu tạo đồng chất và cân đối. Mặt đĩa được chia thành 12 hình quạt bằng nhau và được đánh số từ 1 đến 12. Trọng quay đĩa quanh trục gắn ở tâm 3 lần và quan sát xem mỗi khi dừng lại mũi tên chỉ vào ô ghi số mấy. Tính xác suất của các biến cố:
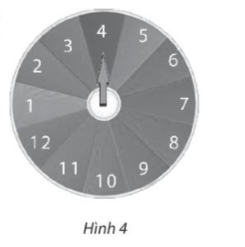
A: “Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ”;
B: “Có đúng 2 lần mũi tên chỉ vào ô ghi số lẻ";
C: “Tích 3 số mũi tên chỉ vào là số nguyên tố”.
Bài tập 6. Một văn phòng A có 15 nhân viên nam và 20 nhân viên nữ. Để khảo sát mức độ hài lòng của nhân viên thông qua hình thức phỏng vấn, người ta lần lượt ghi tên của từng nhân viên vào 35 mẫu giấy giống nhau, từ đó chọn ngẫu nhiên 5 mẩu giấy.
a) Tính xác suất của các biến cố:
A: “Trong 5 người được chọn có 2 nam, 3 nữ”;
B: “Có nhiều nhân viên nữ được chọn hơn nhân viên nam”;
C: “Có ít nhất một người được chọn là nữ”.
b) Biết chị Lan là một nhân viên của văn phòng A. Tính xác suất của biến cố chị Lan được chọn.
Bài tập 7. Một hội đồng có đúng 1 người là nữ. Nếu chọn ngẫu nhiên 2 người từ hội đồng thì xác suất cả hai người đều là nam là 0,8.
a) Chọn ngẫu nhiên 2 người từ hội đồng, tính xác suất của biến cố có 1 người nữ trong 2 người đó.
b) Hội đồng có bao nhiêu người?
Bài tập 8. An, Bình, Cường và 2 bạn nữa xếp ngẫu nhiên thành một hàng ngang để chụp ảnh. Tính xác suất của các biến cố:
a) “An và Bình đứng ở hai đầu hàng";
b) “Bình và Cường đứng cạnh nhau”;
c) “An, Bình, Cường đứng cạnh nhau".
Bài tập 9. Một hộp kín có 1 quả bóng xanh và 5 quả bóng đỏ có kích thước và khối lượng bằng nhau. Hỏi Dũng cần lấy ra từ hộp ít nhất bao nhiêu quả bóng để xác suất lấy được quả bóng xanh lớn hơn 0,5?
Bài tập 10. Bốn đội bóng A, B, C, D lọt vào vòng bán kết của một giải đấu. Ban tổ chức bốc thăm chia 4 đội này thành 2 cặp đấu một cách ngẫu nhiên. Tính xác suất của biến cố hai đội A và B đấu với nhau ở trận bán kết.




