Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo Bài tập cuối chương VII
Hướng dẫn giải bài tập cuối chương VII trang 19 sách bài tập (SBT) toán lớp 10 tập 2
Bài tập cuối chương VII trang 19 sách bài tập (SBT) toán lớp 10 tập 2 là một bài tập khá thú vị và hữu ích. Đây là một phần trong bộ sách "Chân trời sáng tạo" được biên soạn theo chương trình đổi mới của Bộ giáo dục.
Trước tiên, để giải bài tập này, bạn cần đọc kỹ đề bài và hiểu rõ yêu cầu. Sau đó, áp dụng những kiến thức đã học để tìm ra cách giải phù hợp. Khuyến khích bạn tự tìm hiểu và suy nghĩ logic để giải quyết bài tập.
Để làm cho bài tập dễ hiểu hơn, hãy chú ý đến từng bước giải chi tiết và minh họa cụ thể. Hãy tự tin và kiên nhẫn, biết rằng mỗi bước giải bài tập là một cơ hội để bạn học hỏi và phát triển tư duy logic.
Hy vọng rằng, qua hướng dẫn chi tiết này, bạn sẽ nắm vững kiến thức và trở thành một học sinh thông minh và thành công. Chúc bạn thành công trong việc giải bài tập!
Bài tập và hướng dẫn giải
A. Trắc nghiệm
Bài tập 1. Tam thức bậc hai nào có biệt thức $\Delta = 1$ và hai nghiệm là: $x_{1} = \frac{3}{2}$ và $x_{2} = \frac{7}{4}$?
A. $8x^{2} - 26x + 21$; B. $4x^{2} - 13x + \frac{21}{2}$;
C. $4x^{2} + 4x - 15$; D. $2x^{2} - 7x + 6$;
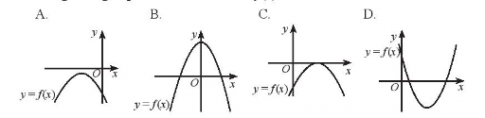
Bài tập 2. Tam thức bậc hai nào đương với mọi x $\in \mathbb{R}$?
A. $2x^{2} - 4x + 2$; B. $3x^{2} + 6x + 2$;
C. $-x^{2} + 2x + 3$; D. $5x^{2} - 3x + 1$.
Bài tập 3. Khẳng định nào sau đây đúng với tam thức bậc hai ƒ(x) = $10x^{2} - 3x - 4$?
A. f(x) > 0 với mọi x không thuộc khoảng (-1; 1);
B. f(x) < 0 với mợi x thuộc khoảng (-1; 1);
C. f(x) $\geq$ 0 với mọi x thuộc khoảng $(-\frac{1}{2}; \frac{4}{5})$;
D. Các khẳng định trên đều sai.
Bài tập 4. Trong trường hợp nào tam thức bậc hai f(x) = $ax^{2} + bx + c$ có $\Delta$ > 0 và a < 0?
Bài tập 5. Cho đồ thị của hàm số bậc hai y = f(x) như Hình 1. Tập nghiệm của bất phương trình ƒ(x) $\geq$ 0 là:
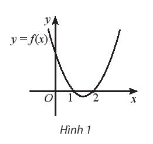
A. (1; 2); B. [1; 2];
C. $(-\infty; 1) \cup (2; +\infty)$; D. $(-\infty; 1] \cup [2; +\infty)$.
Bài tập 6. Bất phương trình nào có tập nghiệm là (2; 5)?
A. $x^{2} - 7x + 10 > 0$; B. $x^{2} - 7x + 10 < 0$;
C. $x^{2} + 13x - 30 > 0$; D. $x^{2} + 13x - 30 > 0$.
Bài tập 7. Tập xác định của hàm số $y = \frac{1}{\sqrt{9x^{2} - 3x - 2}} + \sqrt{3 - x}$ là:
A. $(-\infty; -\frac{1}{3}) \cup (\frac{2}{3}; +\infty)$; B. $(-\infty; -\frac{1}{3}) \cup (\frac{2}{3}; +\infty]$;
C. $(-\infty; -\frac{1}{3}) \cup (3; +\infty)$; D. $(-\frac{1}{3}); 3]$.
Bài tập 8. Với giá trị nào của tham số m thì phương trình $(2m + 6)^{2} + 4mx + 3 = 0$ có hai nghiệm phân biệt?
A. $m < -\frac{3}{2}$ hoặc m > 3; B. $-\frac{3}{2} < m < 3$;
C. m < -3 hoặc $-3 < m < -\frac{3}{2}$ hoặc m > 3; D. $-3 < m < -\frac{3}{2}$ hoặc m > 3.
Bài tập 9. Giá trị nào là nghiệm của phương trình $\sqrt{x^{2} + x + 11} = \sqrt{-2x^{2} - 13x + 16}$?
A. x = - 5; B. $x = \frac{1}{3}$
C. Cả hai câu A, B đều đúng; D. Cả hai câu A, B đều sai.
Bài tập 10. Khẳng định nào đúng với phương trình $\sqrt{2x^{2} - 3x - 1} = \sqrt{3x^{2} - 2x - 13}$ ?
A. Phương trình có hai nghiệm phân biệt cùng dấu;
B. Phương trình có hai nghiệm phân biệt trái dấu;
C. Phương trình có một nghiệm;
D. Phương trình vô nghiệm.
Bài tập 11. Khẳng định nào đúng với phương trình $\sqrt{5x^{2} + 27x + 36} = 2x + 5$ ?
A. Phương trình có một nghiệm;
B. Phương trình vô nghiệm;
C. Tổng các nghiệm của phương trình là -7;
D. Các nghiệm của phương trình đền không bé hơn $-\frac{5}{2}$
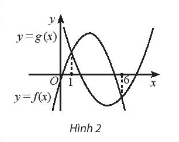
Bài tập 12. Cho đồ thị của hai hàm sô bậc hai f(x) = $ax^{2} + bx + c$ và g(x) = $dx^{2} + ex + h$ như Hình 2. Khẳng định nào đúng với phương trình $\sqrt{ax^{2} + bx + c} = \sqrt{dx^{2} + ex + h}$ ?
A. Phương trình có hai nghiệm phân biệt là x = 1 và x = 6;
B. Phương trình có 1 nghiệm là x = 1;
C. Phương trình có 1 nghiệm là x = 6;
D. Phương trình vô nghiệm.
B. Tự luận
Bài tập 1. Dựa vào đồ thị của hàm số bậc hai y = f(x) sau đây, hãy xét dấu của tam thức bậc hai f(x).
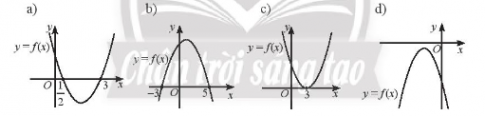
Bài tập 2. Xét dấu của các tam thức bậc hai sau:
a) f(x) = $-7x^{2} + 44x - 45$; b) f(x) = $4x^{2} + 36x + 81$;
c) f(x) = $9x^{2} - 6x + 3$; d) f(x) = $-9x^{2} + 30x - 25$;
e) f(x) = $x^{2} - 4x + 3$; g) f(x) = $-4x^{2} + 8x - 7$;
Bài tập 3. Giải các bất phương trình bậc hai sau:
a) $x^{2} - 10x + 24 \geq 0$; b) $-4x^{2} + 28x - 49 \leq 0$;
c) $x^{2} - 5x + 1 > 0$; d) $9x^{2} - 24x + 16 \leq 0$;
e) $15x^{2} - x - 2 < 0$; g) $-x^{2} + 8x - 17 > 0$;
h) $25x^{2} + 10x - 1 < 0$; i) $4x^{2} + 4x + 7 \leq 0$;
Bài tập 4. Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
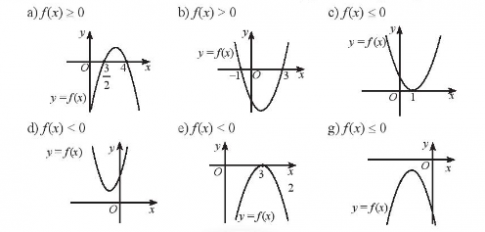
Bài tập 5. Giải các phương trình sau:
a) $\sqrt{3x^{2} + 7x - 1} = \sqrt{6x^{2} + 6x - 11}$; b) $\sqrt{x^{2} + 12x + 28} = \sqrt{2x^{2} + 14x + 24}$;
c) $\sqrt{2x^{2} - 12x - 14} = \sqrt{5x^{2} - 26x - 6}$; d) $\sqrt{11x^{2} - 43x + 25} = - 3x + 4$;
e) $\sqrt{-5x^{2} - x + 35} = x + 5$; g) $\sqrt{11x^{2} - 64x + 97} = 3x - 11$.
Bài tập 6. Tìm tập xác định của các hàm số sau:
a) y = $\sqrt{-x^{2} + 6x - 2}$; b) y = $\frac{2x}{x - 2} + \sqrt{-x^{2} + 3x - 2}$.
Bài tập 7. Tìm các giá trị của tham số m để:
a) f(x) = $(m - 3)^{2} + 2mx - m$ là một tam thức bậc hai âm với mọi x $\in \mathbb{R}$;
b) f(x) = $(m - 2)^{2} + 2(m + 3)x + 5(m - 3)$ là một tam thức bậc hai có nghiệm;
c) Phương trình $2x^{2} + (3m - 1)x + 2(m + 1) = 0$ vô nghiệm;
d) Bất phương trình $2x^{2} + 2(m - 3)x + 3(m^{2} - 3) \geq 0$ có tập nghiệm là $\in \mathbb{R}$.
Bài tập 8. Người la thử nghiệm ném một quả bóng trên Mặt Trăng. Nếu quả bóng được ném lên từ độ cao $h_{o}$ (m) so với bề mặt của Mặt Trăng với vận tốc $v_{o}$ (m/s) thì độ cao của bóng sau t giây được cho bởi hàm số h(t) = $-\frac{1}{2}gt^{2} + v_{o}t + h_{o}$ với g = 1,625 m/$s^{2}$ là gia tốc trọng trường của Mặt Trăng.
a) Biết độ cao ban đầu của quả bóng vào các thời điểm 8 giây và 12 giây lần lượt là 30 m và 5 m, hãy tìm vận tốc ném, độ cao ban đầu của quả bóng và viết công thức h(t).
b) Quả bóng đạt độ cao trên 29 m trong bao nhiêu giây?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Bài tập 9. Mội người phát cầu qua lưới từ độ cao $y_{o}$ mét, nghiêng mội góc $\alpha$ so với phương ngang với vận tốc đầu $v_{o}$.
Phương trình chuyển động của quả cầu là:
y = $\frac{-g}{2v_{o}^{2}cos^{2}\alpha}x^{2} + tan(\alpha)x + y_{o}$ với g = 10 m/$s^{2}$
a)Viết phương trình chuyển động của quả cầu nếu $\alpha = 45_{o}$, $y_{o} = 0,3$ m và v_{o} = 7,67$ m/s.
b) Để cầu qua được lưới bóng cao 1,5m thì người phát câu phải đứng cách lưới bao xa?
Lưu ý: Đáp số làm tròn đến hàng phần trăm.
Bài tập 10. Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD 6.
a) Biểu diễn độ đài cạnh AC và AD theo x.
b) Tìm x để chu vi của tam giác ABC là 12.
c) Tìm x để AD = 2AC.