Giải bài tập toán lớp 8 chân trời sáng tạo bài Bài tập cuối chương 3

Câu hỏi trắc nghiệm

Bài tập 1 trang 88 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó 2 đoạn tre dài 60 cm và 80 cm để làm đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều. Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là

A. 5 m

B. 1 m

C. 1.5 m

D. 2 m

Bài tập 2 trang 88 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thang cân ABCD (AB // CD) có $\widehat{A}=65^{\circ}$. Số đo góc C là:

A. $115^{\circ}$

B. $95^{\circ}$

C. $65^{\circ}$

D. $125^{\circ}$

Bài tập 3 trang 88 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong khẳng định sau, khẳng định nào sai?

A. Tứ giác có ba góc vuông là hình chữ nhật

B. Hình bình hành có một góc vuông là hình chữ nhật

C. Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình chữ nhật

D. Tứ giác có các cạnh đối bằng nhau là hình bình hành.

Bài tập 4 trang 88 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tam giác ABC vuông tại A, đường trung tuyến AM. BIết AB = 8 cm, AC = 15 cm. Độ dài đoạn AM là:

A. 8.5 cm

B.  8 cm

C. 7 cm

D. 7.5 cm

Bài tập 5 trang 88 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thoi ABCD có cạnh bằng 13 cm, độ dài đường chéo AC = 10 cm. Độ dài đường chéo BD là

A. 24 cm

B. 12 cm

C. 16 cm

D. 20 cm

Bài tập 6 trang 88 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các khẳng định sau, khẳng định nào đúng?

A. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông

B. Hình thoi có hai đường chéo vuông góc là hình vuông

C. Hình thoi có một góc vuông là hình vuông

D. Hình chữ nhật có một góc vuông là hình vuông

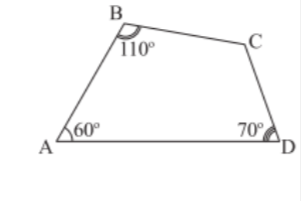
Bài tập 7 trang 88 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tứ giác ABCD, biết $\widehat{A}=60^{\circ},\widehat{B}=110^{\circ},\widehat{D}=70^{\circ}$. Khi đó số đo góc C là

A. $120^{\circ}$

B. $110^{\circ}$

C. $130^{\circ}$

D. $80^{\circ}$

Bài tập tự luận

Bài tập 8 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD, N là giao điểm của DE và AB. Chứng minh rằng:

a) M, N theo thứ tự là trung điểm của CD, AB

b) EMFN là hình bình hành

Bài tập 9 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.

a) Chứng minh rằng tứ giác ADHC là hình thang.

b) Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tứ giác AHBE là hình chữ nhật.

c) Tia CD cắt AH ở M và cắt BE ở N. Chứng minh tứ giác AMBN là hình bình hành.

Bài tập 10 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.

a) Chứng minh tứ giác ANEB là hình thang vuông.

b) Chứng minh tứ giác ANEM là hình chữ nhật.

c) Đường thẳng song song với BN kẻ từ M cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.

d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF.

Bài tập 11 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi I là giao điểm của AF và DE, K là giao điểm của BF và CE.

Chứng minh rằng:

a) Tứ giác AECF là hình bình hành.

b) Tứ giác AEFD là hình gì ? Vì sao ?

c) Chứng minh tứ giác EIFK là hình chữ nhật.

d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.

Bài tập 12 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.

a) Tứ giác MNCD là hình gì ?

b) Chứng minh tam giác EMC cân tại M

c) Chứng minh : $\widehat{BAD}=2\widehat{AEM}$