Giải bài tập toán lớp 8 chân trời sáng tạo bài 1 Định lí Pythagore

1. Định lí Pythagore

Thực hành 1 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ dài cạnh EF, MN của các tam vuông trong Hình 3

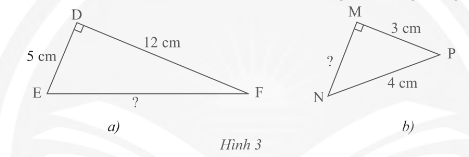
Vận dụng 1 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là 72 cm và 120 cm. Tính độ dài đường chéo của chiếc ti vi đó theo đơn vị inch (biết 1 inch $\approx $ 2.54 cm)

2. Định lí Pythagore đảo

Thực hành 2 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm tam giác vuông trong các tam giác sau:

a) Tam giác EFK có EF = 9m, FK = 12 m, EK = 15 m

b) Tam giác PQR có PQ = 17 cm, QR = 12 cm, PR = 10 cm

c) Tam giác DEF có DE = 8 m, DF = 6 m, EF = 10m

Vận dụng 2 trang 60 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: 

a) Nam dự định làm một cái eke từ ba thanh nẹp gỗ. Nam đã có hai thanh làm hai cạnh góc vuông dài 6 cm và 8 cm. Hỏi thanh nẹp còn lại Nam phải làm có độ dài bao nhiêu? (Giả sử các mối nối không đáng kể).

b) Một khung gỗ ABCD (Hình 6) được tạo thành từ 5 thanh nẹp có độ dài như sau AB = CD = 36 cm; BC = AD = 48 cm; AC = 60 cm. Chứng minh rằng $\widehat{ABC}$ và $\widehat{ADC}$ là các góc vuông.

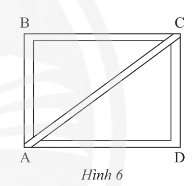
3. Vận dụng định lí Pythagore

Thực hành 3 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính các độ dài PN và BC rong Hình 9

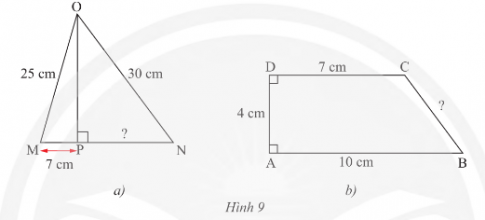
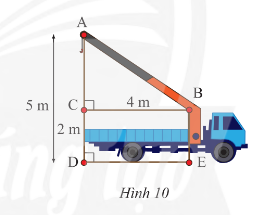
Vận dụng 3 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính ciều dài cần cẩu AB trong Hình 10

Bài tập

Bài tập 1 trang 61 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tam giác ABC vuông tại A.

a) Tính độ dài cạnh BC nếu biết AB = 7 cm, AC = 24 cm

b) Tính độ dài cạnh AB nếu biết AC = 2 cm, BC = $\sqrt{13}$ cm

c) Tính độ dài cạnh AC nếu biết BC = 25 cm, AB = 15 cm

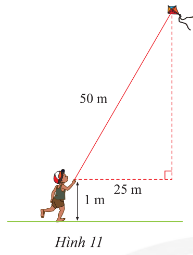
Bài tập 2 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ cao của con diều so với mặt đất (Hình 11).

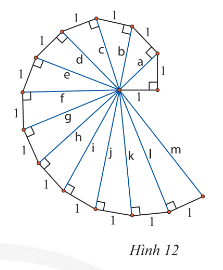
Bài tập 3 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông trong hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại

Bài tập 4 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Chứng minh rằng tam giác ABC vuông trong các trường hợp sau:

a) AB = 8cm, AC = 15cm, BC = 17cm;

b) AB = 29cm, AC = 21cm, BC = 20cm;

c) AB = 12cm, AC = 37cm, BC = 35cm.

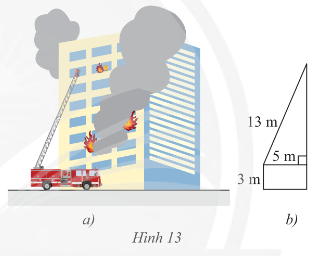
Bài tập 5 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho biết thang của một xe cứu hỏa có chiều dài 13 cm, chân thang cách mặt đất 3m, và cách tường của tòa nhà 5 m. Tính chiều cao mà thang có thể vươn tới.

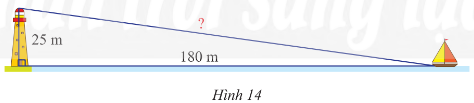
Bài tập 6 trang 62 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180 m. Cho biết tháp hải đăng cao 25 m. Hãy tính khoảng cách từ thuyền đến ngọn hải đăng

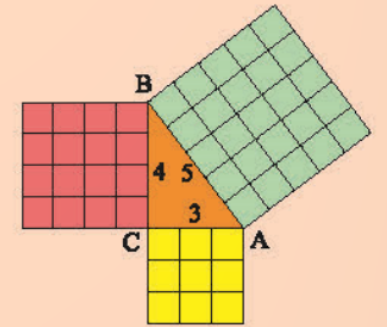
Khởi động trang 58 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Hãy so sánh diện tích hình vuông màu xanh với tổng diện tích của hai hình vuông màu đỏ và màu vàng.

Khám phá 1 trang 58 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho một tam giác vuông có hai cạnh góc vuông là a, b và cạnh huyền là c.

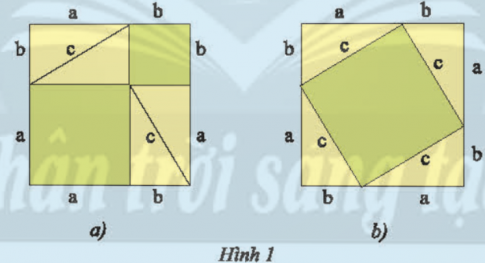
‒ Lấy một tờ bìa lớn, cắt tám hình tam giác vuông bằng tam giác vuông đã cho và cắt hai hình vuông lớn cùng có cạnh bằng a + b.

‒ Đặt bốn tam giác vuông lên hình vuông thứ nhất như trong Hình 1a. Phần bìa không bị che lấp gồm hai hình vuông có cạnh lần lượt là a và b. Tính diện tích phần bìa đó theo a và b.

‒ Đặt bốn tam giác vuông còn lại lên hình vuông thứ hai như trong Hình 1b. Phần bìa không bị che lấp là hình vuông có cạnh là c. Tính diện tích phần bìa đó theo c.

‒ Rút ra kết luận về quan hệ giữa a$^{2}$ + b$^{2}$ và c$^{2}$.

Khám phá 2 trang 59 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Vẽ vào vở tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm, rồi xác định số đo $\widehat{BAC}$ bằng thước đo góc