Giải bài tập toán lớp 8 chân trời sáng tạo bài 4 Hình bình hành - Hình thoi

1. Hình bình hành

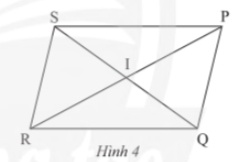
Thực hành 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành PQRS với I là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.

Vận dụng 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mắt lưới của một lưới bóng chuyền có dạng hình tứ giác có các cạnh đối song song. Cho biết độ dài hai cạnh của tứ giác này là 4 cm và 5 cm. Tìm độ dài hai cạnh còn lại.

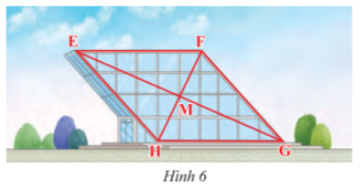
Vận dụng 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt trước của một công trình xây dựng được làm bằng kính có dạng hình bình hành EFGH với M là giao điểm của hai đường chéo (Hình 6). Cho biết EF = 40 m, EM = 36 m, HM = 16 m. Tính độ dài cạnh HG và độ dài hai đường chéo.

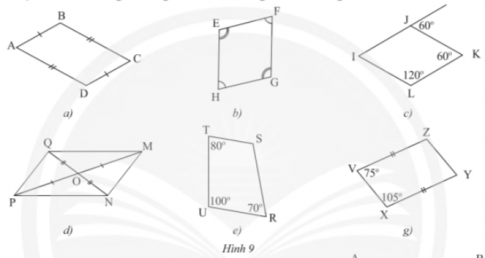
Thực hành 2 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các tứ giác ở Hình 9, tứ giác nào không là hình bình hành?

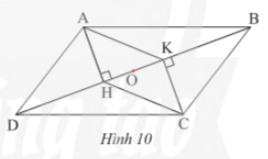
Vận dụng 3 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Quan sát Hình 10, cho biết ABCD và AKCH đều là hình bình hành. Chứng minh ba đoạn thẳng AC, BD và HK có cùng trung điểm O.

2. Hình thoi

Thực hành 3 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thoi MNPQ có I là giao điểm của hai đường chéo.

a) Tính MP khi biết MN = 10 dm, IN = 6 dm

b) Tính $\widehat{IMN}$ khi biết $\widehat{MNP}=128^{\circ}$

Vận dụng 4 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ dài cạnh của các khuy áo hình thoi có độ dài hai đường chéo lần lượt là 3.2 cm và 2.4 cm

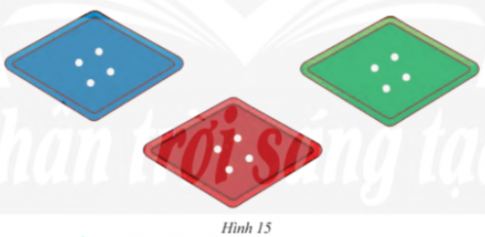
Vận dụng 5 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một hoa văn trang trí được ghép bởi ba hình tứ giác có độ dài mỗi cạnh đều bằng 2 cm (Hình 18). Gọi tên các tứ giác này và tính chu vi của hoa văn

Vận dụng 6 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một tứ giác có chu vi là 52 cm và một đường chéo là 24 cm. Tìm độ dài của mỗi cạnh và đường chéo còn lại nếu hai đường chéo vuông góc tại trung điểm của mỗi đường.

Bài tập

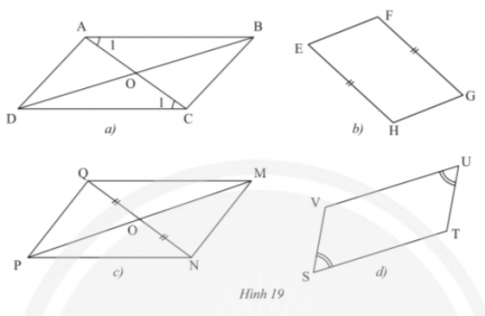
Bài tập 1 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?

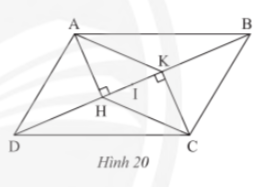
Bài tập 2 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 21)

a) Chứng minh tứ giác AHCK là hình bình hành

b) Gọi I là trung điểm của HK. Chứng minh IB = ID

Bài tập 3 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD. Gọi E là trung điểm AD, F là trung điểm của BC.

a) Chứng minh rằng tứ giác EBFD là hình bình hành.

b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng

Bài tập 4 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF.

b) Tứ giác DEBF là hình gì ?

Bài tập 5 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD, E và F là giao điểm của AK và CI với BD.

a) Chứng minh tứ giác AKCI là hình bình hành.

b) Chứng minh rằng DE = EF = FB.

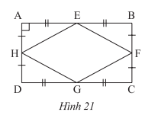
Bài tập 6 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình 21. Chứng minh rằng tứ giác EFGH là hình thoi.

Bài tập 7 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.

Bài tập 8 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.

a) Chứng minh tứ giác ABCD là hình thoi.

b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau

b) Chứng minh tứ giác AEMF là hình thoi.

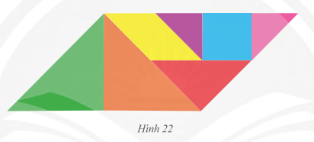
Bài tập 9 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm các hình bình hành và hình thang có trong Hình 22

Khởi động trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Quan sát hình chụp các mái nhà ở phố cổ Hội An, em thấy các cạnh đối của tứ giác ABCD có gì đặc biệt?

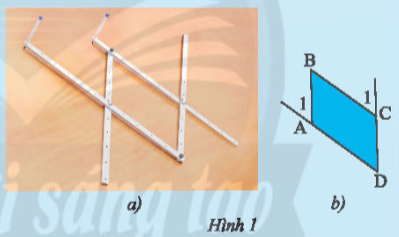
Khám phá 1 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc $\widehat{A_{1}}$ và $\widehat{D}$, $\widehat{C_{1}}$ và $\widehat{D}$ của tứ giác ABCD (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh AB và CD; AD và BC.

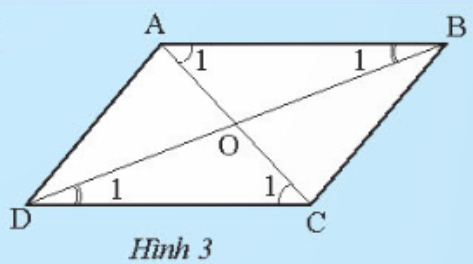
Khám phá 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:

‒ Tam giác ABC bằng tam giác CDA.

‒ Tam giác OAB bằng tam giác OCD.

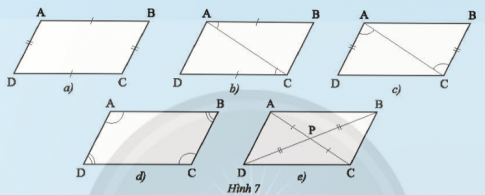
Khám phá 3 trang 75 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tứ giác ABCD có P là giao điểm của hai đường chéo. Giải thích tại sao AB // CD và AD // BC trong mỗi trường hợp sau:

Trường hợp 1: AB = CD và AD = BC (Hình 7a).

Trường hợp 2: AB // CD và AB = CD (Hình 7b).

Trường hợp 3: AD // BC và AD = BC (Hình 7c).

Trường hợp 4: $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$ (Hình 7d).

Trường hợp 5: PA = PC, PB = PD (Hình 7e).

Khám phá 4 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Hình 11a là hình chụp tấm lưới thép được đan thành nhiều mắt. Hình 11b là hình vẽ phóng to của một mắt lưới. Đo độ dài các cạnh của tứ giác ABCD và rút ra nhận xét.

Khám phá 5 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: 

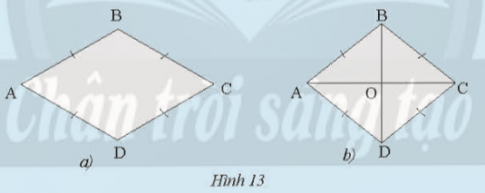
a) Hình thoi có là hình bình hành không?

b) Cho hình thoi ABCD có O là giao điểm của hai đường chéo (Hình 13b). Các tam giác OAB, OCB, OCD, OAD có bằng nhau không?

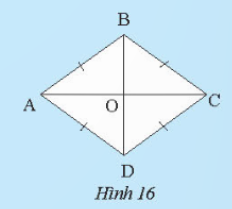
Khám phá 6 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho ABCD là một hình bình hành. Giải thích tại sao tứ giác ABCD có bốn cạnh bằng nhau trong mỗi trường hợp sau:

Trường hợp 1: AB = AD.

Trường hợp 2: AC vuông góc với BD.

Trường hợp 3: AC là đường phân giác góc BAD.

Trường hợp 4: BD là đường phân giác góc ABC.