Giải bài tập sách bài tập (SBT) toán lớp 10 kết nối tri thức Bài tập cuối chương VI
Hướng dẫn giải Bài tập cuối chương VI trang 22 sách bài tập (SBT) toán lớp 10
Bài tập cuối chương VI trang 22 sách bài tập (SBT) toán lớp 10 là một phần quan trọng trong quá trình học tập của học sinh. Với cách hướng dẫn cụ thể và giải chi tiết, học sinh sẽ hiểu rõ hơn về bài học này.
Bài tập này nằm trong bộ sách "Kết nối tri thức" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Đây là một công cụ hữu ích giúp học sinh rèn luyện kỹ năng giải toán, từ đó phát triển tư duy logic và phản xạ nhanh nhạy trong việc giải quyết vấn đề.
Hi vọng rằng qua bài tập cuối chương VI trang 22 này, học sinh sẽ mạnh mẽ hơn trong môn toán và cảm thấy tự tin hơn khi đối diện với các bài toán khó khăn hơn trong tương lai.
Bài tập và hướng dẫn giải
A - Trắc nghiệm
6.33. Thu nhập bình quân theo đầu người (GDP) của Việt Nam (tính theo USD) trong vòng 10 năm, từ năm 2009 đến năm 2018 được cho bởi bảng sau (dựa theo số liệu của Tổng cục Thống kê):
Năm | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
GDP | 1055 | 1273 | 1517 | 1749 | 1908 | 2052 | 2109 | 2215 | 2385 | 2587 |
Bảng này xác định một hàm số chỉ sự phụ thuộc của GDP (kí hiệu là y) vào thời gian x (tính bằng năm). Khẳng định nào dưới đây là sai?
A. Giá trị của hàm số tại x = 2018 là 2 587;
B. Tập xác định của hàm số có 10 phần tử;
C. Tập giá trị của hàm số có 10 phần tử;
D. Giá trị của hàm số tại x = 2 587 là 2018.
6.34. Các đường dưới đây, đường nào không là đồ thị của hàm số ?

6.35. Tập xác định của hàm số $y=\sqrt{x}$ là
A. ℝ\{0};
B. ℝ;
C. [0; +∞);
D. (0; +∞).
6.36. Hàm số $y=\frac{1}{x}$ có
A. Tập xác định là ℝ\{0} và tập giá trị là ℝ;
B. Tập xác định và tập giá trị cùng là ℝ\{0};
C. Tập xác định là ℝ và tập giá trị là ℝ\{0};
D. Tập xác định và tập giá trị cùng là ℝ.
6.37. Với những giá trị nào của m thì hàm số f(x) = (m + 1)x + 2 đồng biến trên ℝ ?
A. m > –1;
B. m = 1;
C. m < 0;
D. m = 0.
6.38. Đồ thị trong hình vẽ dưới đây là của hàm số nào?

A. $y=|\frac{1}{2}x|$;
B. y = |3 – x|;
C. y = |x|;
D. y = |2x|.
6.39. Trục đối xứng của parabol (P): $y = 2x^{2} + 6x + 3 $là
A. y = –3;
B.$ y=-\frac{3}{2}$
C. x = –3;
D.$x=-\frac{3}{2}$x=−32">
6.40. Parabol $y = –4x – 2x^{2}$ có đỉnh là
A. I(–1; 1);
B. I(–1; 2);
C. I(1; 1);
D. I(2; 0).
6.41. Cho hàm số $y = x^{2} – 2x + 3$. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên (–∞; 2);
B. Hàm số nghịch biến trên (–∞; 2);
C. Hàm số đồng biến trên (–∞; 1);
D. Hàm số nghịch biến trên (–∞; 1).
6.42. Đường parabol trong hình dưới đây là đồ thị của hàm số nào ?
$A. y = x^{2} + 2x – 3;$
$B. y = –x^{2} – 2x + 3;$
$C. y = –x^{2} + 2x – 3;$
$D. y = x^{2} – 2x – 3.$
6.43. Cho hàm số bậc hai $y = ax^{2} + bx + c$ có đồ thị là đường parabol dưới đây. Khẳng định nào dưới đây là đúng?
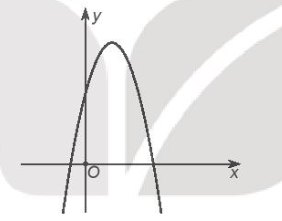
A. a < 0, b < 0, c < 0;
B. a < 0, b < 0, c > 0;
C. a < 0, b > 0, c < 0;
D. a < 0, b > 0, c > 0.
6.44. Điều kiện cần và đủ của tham số m để parabol (P): $y = x^{2} – 2x + m – 1 $ cắt trục Ox tại hai điểm phân biệt nằm về hai phía của trục tung là
A. m < 1;
B. m < 2;
C. m > 2;
D. m > 1.
6.45. Bảng xét dấu dưới đây là của tam thức bậc hai nào?
x | $-\infty $ |
| -2 |
| 3 |
| $+\infty $ |
F(x) |
| - | 0 | + | 0 | - |
|
A. $f(x) = –x^{2} + x + 6;$
B. $f(x) = x^{2} – x – 6;$
C. $f(x) = –x^{2} + 5x – 6; $
D. $f(x) = x^{2}– 5x + 6.$
6.46. Bảng xét dấu nào sau đây là bảng xét dấu của tam thức $f(x) = x^{2} + 12x + 36$ ?
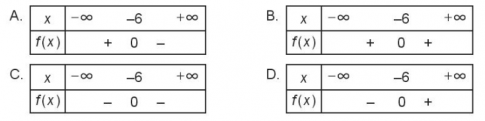
6.47. Tập nghiệm của bất phương trình $x^{2}– 4x + 3 < 0$ là
A. (1; 3);
B. (–∞; 1)∪[3; +∞);
C. [1; 3];
D. (–∞; 1]∪[4; +∞).
6.48. Các giá trị của tham số m làm cho biểu thức $f(x) = x^{2} + 4x + m – 5$ luôn dương là
A. m ≥ 9;
B. m > 9;
C. Không có m;
D. m < 9.
6.49. Phương trình $(m + 2) x^{2} – 3x + 2m – 3 = 0$ có hai nghiệm trái dấu khi và chỉ khi
A. m < –2 hoặc $m>\frac{3}{2}$;
B. $m>\frac{3}{2}$;
C. $-2<m<\frac{3}{2}$;
D. m < 2.
6.50. Bất phương trình $mx^{2} – (2m – 1)x + m + 1 < 0$ vô nghiệm khi và chỉ khi
A. $m\leq \frac{1}{8}$;
B. $m> \frac{1}{8}$;
C. $m<\frac{1}{8}$;
D. $m\geq \frac{1}{8}$;
6.51. Số nghiệm của phương trình $\sqrt{x^{2}+4x-2}=x-3$ là
A. 0;
B. 1;
C. 2;
D. 3.
6.52. Tập nghiệm của phương trình $\sqrt{2x^{2}-9x-9}=3-x$ là
A. S = {6};
B. S = ∅;
C. S = {–3};
D. S = {–3; 6}.
6.53. Tập nghiệm của phương trình $\sqrt{2x^{2}-5x+1}=\sqrt{x^{2}+2x-9}$ là
A. S = {2};
B. S = {5};
C. S = ∅;
D. S = {2; 5}.
B - Tự luận
6.54. Tìm tập xác định của các hàm số sau:
a) $y=\sqrt{-x^{2}+3x-2}$;
b) $y=\frac{x-1}{\sqrt{x^{2}-1}}$.
6.55. Cho hàm số $y=\left\{\begin{matrix}2x+3 khi -2\leq <-1 \\ \frac{1}{2}x+\frac{3}{2} khi -1\leq x<1\\ -\frac{1}{2}x+\frac{9}{2} khi 1\leq x\leq 3\end{matrix}\right.$
a) Tìm tập xác định của hàm số.
b) Vẽ đồ thị hàm số.
c) Từ đồ thị vẽ ở ý b) hãy chỉ ra các khoảng đồng biến, khoảng nghịch biến của hàm số.
d) Tìm tập giá trị của hàm số.
6.56. Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập xác định, tập giá trị, khoảng đồng biến và khoảng nghịch biến của chúng.
a) y = |x – 1| + |x + 1|;
b) $y=\left\{\begin{matrix}x+1 khi x<-1\\ x^{2}-1 khi x\geq -1\end{matrix}\right.$
6.57. Dựa vào đồ thị của hàm số $y = ax^{2} + bx + c$, hãy xác định dấu của các hệ số a, b, c trong mỗi trường hợp dưới đây.

6.58. Trong mỗi trường hợp dưới đây, hãy vẽ đồ thị của các hàm số trên cùng một mặt phẳng toạ độ rồi xác định toạ độ giao điểm của chúng:
a) y = –x + 3 và $y = –x^{2} – 4x + 1.$
b) y = 2x – 5 và $y = x^{2} – 4x – 1.$
6.59. Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình tương ứng
a) $y = x^{2} – 3x + 2$ và bất phương trình: $x^{2} – 3x + 2 ≥ 0;$
b) $y = x^{2} – x – 6 $ và bất phương trình: $x^{2} – x – 6 < 0.$
6.60. Tìm các giá trị của tham số m để:
a) Hàm số $\frac{1}{\sqrt{mx^{2}-2mx+5}}$ có tập xác định ℝ;
b) Tam thức bậc hai $y = –x^{2} + mx – 1$ có dấu không phụ thuộc vào x;
c) Hàm số $y=\sqrt{-2x^{2}-mx-m-6}$ có tập xác định chỉ gồm một phần tử.
6.61. Cho hình chữ nhật ABCD có AB = 6 cm, AD = 13 cm. Tìm vị trí điểm M trên cạnh AD sao cho BM = 2MD.
6.62. Trong Vật lí ta biết rằng, khi một vật được ném xiên với vận tốc ban đầu v0, góc ném hợp với phương ngang Ox một góc α, nếu ta bỏ qua sức cản của không khí và gió, vật chỉ chịu tác động của trọng lực với gia tốc trọng trường $g ≈ 9,8 m/s^{2}$, thì độ cao y (so với mặt đất) của vật phụ thuộc vào khoảng cách theo phương ngang x (tính đến mặt đất tại điểm ném) theo một hàm số bậc hai cho bởi công thức
$y=\frac{-g}{2v_{0}^{2}cos^{2}\alpha }x^{2}+xtan\alpha $
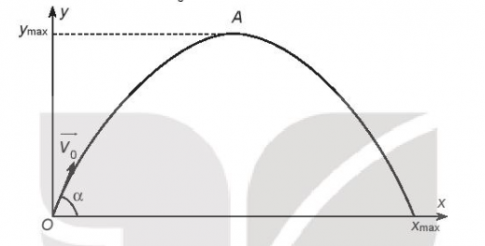
Như vậy quỹ đạo chuyển động của vật là một phần của đường parabol. Hãy xác định
a) Các hệ số a, b và c của hàm số bậc hai này;
b) Độ cao lớn nhất mà vật có thể đạt được;
c) Giả sử vận tốc ban đầu v0 không đổi. Từ kết quả câu b) hãy xác định góc ném α để độ cao lớn nhất của vật đạt giá trị lớn nhất.
d) Một quả bóng được đá từ mặt đất lên cao với vận tốc ban đầu v0 = 20 m/s và góc đá so với phương ngang là α = 45°. Khi quả bóng ở độ cao trên 5 m thì khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí đá bóng nằm trong khoảng nào (làm tròn kết quả đến hàng phần trăm) ?
6.63. Một công ty kinh doanh máy tính cầm tay thấy rằng khi bán máy ở mức giá x (nghìn đồng) một chiếc thì số lượng máy bán được n cho bởi phương trình n = 1200000 – 1200x.
a) Tìm công thức biểu diễn doanh thu R như là hàm số của đơn giá x. Tìm miền xác định của hàm số R = R(x).
b) Máy tính được bán ở đơn giá nào sẽ cho doanh thu lớn nhất ? Tính doanh thu lớn nhất và số máy tính bán được trong trường hợp đó.
c) Với đơn giá nào thì công ty sẽ đạt được doanh thu trên 200 tỉ đồng (làm tròn đến nghìn đồng) ?





