Giải bài tập sách bài tập (SBT) toán lớp 10 kết nối tri thức bài 18 Phương trình quy về phương trình bậc hai
Hướng dẫn giải bài 18 Phương trình quy về phương trình bậc hai
Trong vở bài tập trang 21 sách bài tập (SBT) toán lớp 10, chúng ta sẽ học cách giải các bài tập liên quan đến phương trình quy về phương trình bậc hai. Đây là một phần quan trọng trong chương trình đổi mới của Bộ giáo dục. Việc giải bài tập này giúp học sinh hiểu rõ hơn về phương trình bậc hai và cách giải quyết các vấn đề liên quan.
Qua cách hướng dẫn cụ thể và giải chi tiết trong vở bài tập, hy vọng học sinh sẽ có thể nắm bắt kiến thức một cách tốt nhất. Việc thực hành giải bài tập từ bài 18 này sẽ giúp học sinh rèn luyện kỹ năng giải toán và phát triển tư duy logic.
Với sự hỗ trợ của sách bài tập (SBT) toán lớp 10 và cách hướng dẫn chi tiết, chúng ta sẽ cùng nhau vượt qua phần bài tập này một cách hiệu quả và hiểu bài hơn. Chúc các bạn thành công!
Bài tập và hướng dẫn giải
BÀI TẬP
6.28. Giải các phương trình sau:
a) $\sqrt{-x^{2}+77x-212}=\sqrt{x^{2}+x-2}$
b) $\sqrt{x^{2}+25x-26}=\sqrt{x-x^{2}}$
c) $\sqrt{4x^{2}+8x-37}=\sqrt{-x^{2}-2x+3}$
6.29. Giải các phương trình sau:
a) $\sqrt{2x^{2}-13x+16}=6-x$;
b) $\sqrt{3x^{2}-33x+55}=x-5$;
c) $\sqrt{-x^{2}+3x+1}=x-4$.
2.30. Giải các phương trình sau:
a) $\sqrt{2x-3}=x-3$
b) $(x-3)\sqrt{x^{2}+4}=x^{2}-9$
6.31. Tìm điều kiện của tham số m để phương trình sau có nghiệm: $\sqrt{2x^{2}+x+1}=\sqrt{x^{2}+mx+m-1}$ (1)
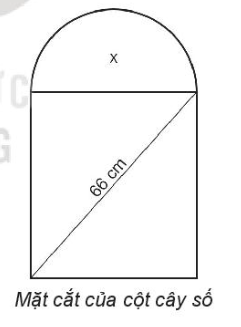
6.32. Mặt cắt đứng của cột cây số trên quốc lộ có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật (xem hình dưới). Biết rằng đường kính của nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 66 cm. Tìm kích thước của hình chữ nhật, biết rằng diện tích của phần nửa hình tròn bằng 0,3 lần diện tích của phần hình chữ nhật. Lấy π = 3,14 và làm tròn kết quả đến chữ số thập phân thứ hai.
