Giải bài tập sách bài tập (SBT) toán lớp 10 kết nối tri thức bài 22 Ba đường conic
Hướng dẫn giải bài 22 Ba đường conic trang 46 sách bài tập (SBT) toán lớp 10
Trong bài 22 này, chúng ta sẽ tìm hiểu về ba đường conic, bao gồm parabol, hyperbol và elip. Đây là những đường cong quen thuộc trong toán học và có nhiều ứng dụng trong thực tế.
Đầu tiên, để giải bài toán liên quan đến ba đường conic, chúng ta cần nắm vững đặc điểm của từng loại đường con. Parabol có hình dáng giống hình chữ U, hyperbol có hai nhánh cong và elip có hình dáng oval.
Tiếp theo, chúng ta sẽ áp dụng kiến thức đã nắm để giải các bài tập liên quan đến ba đường conic. Việc áp dụng lý thuyết vào bài tập sẽ giúp chúng ta hiểu sâu hơn về đặc điểm và tính chất của mỗi loại đường conic.
Qua bài toán này, hy vọng các bạn sẽ nắm vững kiến thức về ba đường conic và có thể áp dụng vào các bài tập khác trong tương lai. Hãy cố gắng làm bài thật kỹ và chính xác để hiểu rõ hơn về chủ đề này.
Bài tập và hướng dẫn giải
BÀI TẬP
7.28. Cho elip (E) có phương trình $\frac{x^{2}}{36}+\frac{y^{2}}{16}=1$. Tìm tiêu điểm và tiêu cự của elip.
7.29. Cho hypebol (H) có phương trình $\frac{x^{2}}{16}-\frac{y^{2}}{20}=1$. Tìm tiêu điểm và tiêu cự của hypebol.
7.30. Cho parabol (P) có phương trình $y^{2}$ = 4x. Tìm tiêu điểm và đường chuẩn của parabol.
7.31. Viết phương trình chính tắc của elip (E), biết (E) đi qua điểm A(6; 0) và có tiêu cự bằng 8.
7.32. Viết phương trình chính tắc của hypebol (H), biết (H) đi qua điểm $M(3\sqrt{2};-4)$ và có một tiêu điểm là F2(5;0)
7.33. Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng Δ: x + 4 = 0. Tìm toạ độ điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của (P) bằng 5.
7.34. Cho parabol (P) có phương trình là y$^{2}$ = 16x. Gọi Δ là đường thẳng bất kì đi qua tiêu điểm F của (P) và không trùng với trục hoành. Chứng minh rằng Δ luôn cắt (P) tại hai điểm phân biệt A, B, đồng thời tích các khoảng cách từ A và B đến trục hoành không đổi.
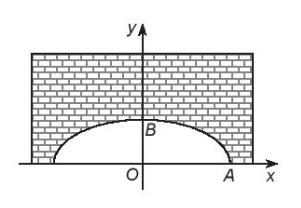
7.35. Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cao 2,8 m có thể đi qua hầm được không?
7.36. Cho điểm M(x0; y0) thuộc elip (E) có phương trình $\frac{x^{2}}{2}+\frac{y^{2}}{1}=1$ .
a) Tính $MF1^{2} – MF2^{2}$ theo x0; y0. Từ đó tính MF1, MF2, theo x0; y0.
b) Tìm điểm M sao cho MF2 = 2MF1.
c) Tìm M sao cho góc nhìn của M tới hai đểm F1; F2 (tức là góc $\widehat{F1MF2}$ ) là lớn nhất ?
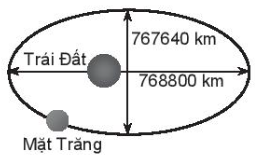
7.37. Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.