6.43.Cho hàm số bậc hai $y = ax^{2}+ bx + c$ có đồ thị là đường parabol dưới đây. Khẳng...
Câu hỏi:
6.43. Cho hàm số bậc hai $y = ax^{2} + bx + c$ có đồ thị là đường parabol dưới đây. Khẳng định nào dưới đây là đúng?
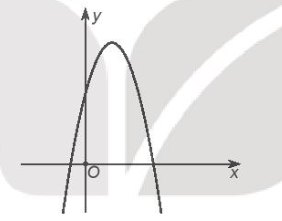
A. a < 0, b < 0, c < 0;
B. a < 0, b < 0, c > 0;
C. a < 0, b > 0, c < 0;
D. a < 0, b > 0, c > 0.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Vương
Phương pháp giải:Để giải bài toán này, chúng ta cần xác định được các hệ số a, b, c mà đồ thị của hàm số bậc hai y = ax^2 + bx + c thỏa mãn điều kiện đã cho.Đầu tiên, vì đồ thị của parabol này hướng lên hay hướng xuống phụ thuộc vào dấu của hệ số a nên ta thực hiện phân tích dấu của a.- Nếu a < 0, thì đồ thị của parabol sẽ có bề lõm hướng xuống.Tiếp theo, ta cần xác định dấu của hệ số c bằng cách xem xét vị trí cắt trục tung của đồ thị parabol.- Nếu c > 0, tức là đồ thị cắt trục tung tại một điểm có tung độ dương.Cuối cùng, để xác định dấu của hệ số b, ta nhìn vào hoành độ của đỉnh parabol. Vì hoành độ của đỉnh là -b/2a, và a < 0 nên điều kiện là -b/2a > 0.- Kết hợp với a < 0, ta có điều b > 0.Vậy, câu trả lời cho câu hỏi trên là: a < 0, c > 0, b > 0.
Câu hỏi liên quan:
- A - Trắc nghiệm6.33.Thu nhập bình quân theo đầu người (GDP) của Việt Nam (tính theo USD)...
- 6.34.Các đường dưới đây, đường nào không là đồ thị của hàm số ?
- 6.35.Tập xác định của hàm số $y=\sqrt{x}$ làA. ℝ\{0};B. ℝ;C. [0; +∞);D. (0; +∞).
- 6.36.Hàm số $y=\frac{1}{x}$cóA. Tập xác định là ℝ\{0} và tập giá trị là ℝ;B. Tập xác...
- 6.37.Với những giá trị nào của m thì hàm số f(x) = (m + 1)x + 2 đồng biến trên ℝ ?A. m >...
- 6.38.Đồ thị trong hình vẽ dưới đây là của hàm số nào?A. $y=|\frac{1}{2}x|$;B. y = |3 – x|;C....
- 6.39.Trục đối xứng của parabol (P): $y = 2x^{2}+ 6x + 3 $làA. y =...
- 6.40.Parabol $y = –4x – 2x^{2}$có đỉnh làA. I(–1; 1);B. I(–1; 2);C. I(1; 1);D....
- 6.41.Cho hàm số $y = x^{2}– 2x + 3$. Mệnh đề nào dưới đây đúng?A. Hàm số đồng biến trên...
- 6.42.Đường parabol trong hình dưới đây là đồ thị của hàm số nào ?$A. y = x^{2}+ 2x –...
- 6.44.Điều kiện cần và đủ của tham số m để parabol (P): $y = x^{2}– 2x + m –...
- 6.45.Bảng xét dấu dưới đây là của tam thức bậc hai nào?x$-\infty...
- 6.46.Bảng xét dấu nào sau đây là bảng xét dấu của tam thức $f(x) = x^{2}+ 12x + 36$ ?
- 6.47. Tập nghiệm của bất phương trình $x^{2}– 4x + 3 < 0$ làA. (1; 3);B. (–∞; 1)∪[3; +∞);C. [1;...
- 6.48.Các giá trị của tham số m làm cho biểu thức $f(x) = x^{2}+ 4x + m – 5$ luôn dương...
- 6.49.Phương trình $(m + 2) x^{2}– 3x + 2m – 3 = 0$ có hai nghiệm trái dấu khi và chỉ...
- 6.50.Bất phương trình $mx^{2}– (2m – 1)x + m + 1 < 0$ vô nghiệm khi và chỉ khiA....
- 6.51.Số nghiệm của phương trình $\sqrt{x^{2}+4x-2}=x-3$làA. 0;B. 1;C. 2;D. 3.
- 6.52.Tập nghiệm của phương trình $\sqrt{2x^{2}-9x-9}=3-x$ làA. S = {6};B. S =∅;C. S =...
- 6.53.Tập nghiệm của phương trình $\sqrt{2x^{2}-5x+1}=\sqrt{x^{2}+2x-9}$làA. S = {2};B....
- B - Tự luận6.54.Tìm tập xác định của các hàm số...
- 6.55.Cho hàm số $y=\left\{\begin{matrix}2x+3 khi -2\leq <-1 \\ \frac{1}{2}x+\frac{3}{2}...
- 6.56.Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập xác định, tập giá trị, khoảng đồng biến...
- 6.57.Dựa vào đồ thị của hàm số $y = ax^{2}+ bx + c$, hãy xác định dấu của các hệ số a,...
- 6.58.Trong mỗi trường hợp dưới đây, hãy vẽ đồ thị của các hàm số trên cùng một mặt phẳng toạ...
- 6.59.Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình tương ứnga) $y =...
- 6.60.Tìm các giá trị của tham số m để:a) Hàm số$\frac{1}{\sqrt{mx^{2}-2mx+5}}$có...
- 6.61.Cho hình chữ nhật ABCD có AB = 6 cm, AD = 13 cm. Tìm vị trí điểm M trên cạnh AD sao cho...
- 6.62.Trong Vật lí ta biết rằng, khi một vật được ném xiên với vận tốc ban đầu v0, góc ném hợp...
- 6.63.Một công ty kinh doanh máy tính cầm tay thấy rằng khi bán máy ở mức giá x (nghìn đồng)...
Bình luận (0)





