Giải bài tập sách bài tập (SBT) toán lớp 8 Cánh diều bài 9 Hình đồng dạng

Bài tập 50 trang 81 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:

Cho tam giác ABC có E, F lần lượt là trung điểm của BC, AC. Các điểm M, P, R, Q lần lượt nằm trên AB, BE, EF, FA sao cho $\frac{BM}{MA}=\frac{QF}{QA}=\frac{RF}{RE}=\frac{BP}{PE}$ = 1,8 (Hình 50).

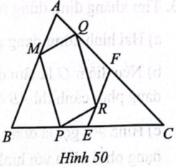
Tìm khẳng định sai trong các khẳng định sau:

a) Hai đoạn thẳng EF và AB đồng dạng phối cảnh, điểm C là tâm đồng dạng phối cảnh.

b) Hai đoạn thẳng MP và AE đồng dạng phối cảnh, điểm B là tâm đồng dạng phối cảnh và $\frac{BM}{BA}=\frac{BP}{BE}=\frac{3}{5}$.

c) Hai đoạn thẳng PR và BF đồng dạng phối cảnh, điểm E là tâm đồng dạng phối cảnh.

Bài tập 51 trang 81 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:

Cho điểm O nằm ngoài tam giác MNP. Trên các tia OM, ON, OP ta lần lượt lấy các điểm M’, N’, P’ sao cho $\frac{OM’}{OM}=\frac{ON’}{ON}=\frac{OP’}{OP}=\frac{5}{3}$ (Hình 51).

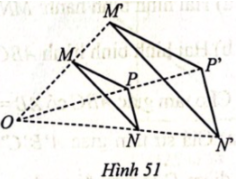
a) Tam giác M’N’P’ có đồng dạng phối cảnh với tam giác MNP hay không? Nếu có, hãy chỉ ra tâm đồng dạng phối cảnh.

b) Hãy chỉ ra đoạn thẳng AB sao cho hai đoạn thẳng AB và MP đồng dạng phối cảnh, điểm O là tâm đồng dạng phối cảnh và $\frac{OA}{OM}=\frac{OB}{OP}=\frac{1}{4}$.

Bài tập 52 trang 82 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:

Quan sát Hình 52, biết các điểm A, B, C, D lần lượt là trung điểm của các đoạn thẳng IA’, IB’, IC’, ID’.

a) Cho biết hai tứ giác ABCD và A’B’C’D’ có đồng dạng phối cảnh hay không? Nếu có, hãy chỉ ra tâm đồng dạng phối cảnh.

b) Tứ giác A’B’C’D’ có là hình chữ nhật hay không, nếu tứ giác ABCD là hình chữ nhật? Vì sao?

Bài tập 53 trang 82 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:

Tìm khẳng định đúng trong các khẳng định sau:

a) Hai hình đồng dạng phối cảnh (hay vị tự) không là hai hình đồng dạng.

b) Nếu điểm O là tâm đồng dạng phối cảnh của hai đoạn thẳng AB và A’B’ đồng dạng phối cảnh thì AB // A’B’.

c) Hình ℌ’ gọi là đồng dạng với hình ℌ nếu hình ℌ’ bằng một hình nào đó đồng dạng phối cảnh với hình ℌ.

Bài tập 54 trang 82 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:

Trong Hình 53, các điểm A, B, C, D lần lượt là các điểm nằm trên các đoạn thẳng IM, IN, IP, IQ sao cho $\frac{IA}{IM}=\frac{IB}{IN}=\frac{IC}{IP}=\frac{ID}{IQ}=\frac{1}{3}$

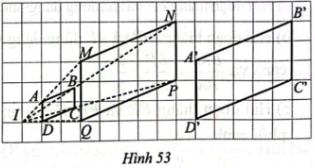
Quan sát Hình 53 và cho biết:

a) Hai hình bình hành MNPQ và A’B’C’D’ có bằng nhau hay không; 

b) Hai hình bình hành ABCD và A’B’C’D’ có đồng dạng hay không.

Bài tập 55 trang 82 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:

Cho tam giác ABC có AB = 13, BC = 14, CA = 15. Cho D, E là hai điểm phân biệt.

a) Giả sử tam giác A’B’C’ là hình đồng dạng phối cảnh của tam giác ABC với điểm D là tâm đồng dạng phối cảnh, tỉ số $\frac{A’B’}{AB}=\frac{4}{5}$. Tìm độ dài các cạnh của tam giác A’B’C’. 

b) Giả sử tam giác A”B”C” là hình đồng dạng phối cảnh của tam giác ABC với điểm E là tâm đồng dạng phối cảnh, tỉ số $\frac{A”B”}{AB}=\frac{4}{5}$.Tìm độ dài các cạnh của tam giác A”B”C”.

c) Chứng minh diện tích tam giác A’B’C’ bằng diện tích tam giác A”B”C”.