Giải bài tập sách bài tập (SBT) toán lớp 8 Cánh diều bài 4 Hình bình hành
Giải bài tập sách bài tập (SBT) toán lớp 8 Cánh diều bài 4 Hình bình hành
Trong bài viết này, chúng ta sẽ cùng nhau đi vào chi tiết giải đề sách bài tập toán lớp 8 Cánh diều bài 4 về hình bình hành. Sytu sẽ hướng dẫn bạn giải mọi câu hỏi và bài tập một cách dễ hiểu và nhanh chóng nhất. Chúng ta hy vọng rằng thông qua bài viết này, các em học sinh sẽ có thể củng cố kiến thức một cách tốt nhất và hiểu rõ hơn về bài học. Hãy cùng nhau khám phá và học hỏi!
Bài tập và hướng dẫn giải
Bài tập 16 trang 94 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho tam giác ABC có AB = AC = 3 cm. Từ điểm M thuộc cạnh BC, kẻ MD song song với AC và ME song song với AB (điểm D, E lần lượt thuộc cạnh AB, AC). Tính chu vi của tứ giác ADME.
Bài tập 17 trang 94 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho tam giác ABC có các đường trung tuyến BD và CE. Lấy các điểm H, K sao cho E là trung điểm của CH, D là trung điểm của BK. Chứng minh:
a) Các tứ giác AHBC, AKCB là hình bình hành;
b) A là trung điểm của HK.
Bài tập 18 trang 95 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho hình bình hành ABCD. Trên cạnh AD, BC lần lượt lấy điểm E, F sao cho AE = CF. Trên cạnh AB, CD lần lượt lấy điểm M, N sao cho BM = DN. Chứng minh:
a) Tứ giác EMFN là hình bình hành;
b) Bốn đường thẳng AC, BD, EF, MN cùng đi qua một điểm.
Bài tập 19 trang 95 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại H. Qua B kẻ tia Bx vuông góc với AB. Qua C kẻ tia Cy vuông góc với AC. Gọi D là giao điểm của Bx và Cy (Hình 15).
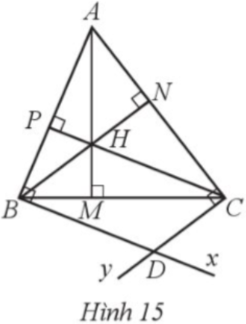
a) Chứng minh tứ giác BDCH là hình bình hành.
b*) Tam giác ABC có điều kiện gì thì ba điểm A, D, H thẳng hàng?
c) Tìm mối liên hệ giữa góc A và góc D của tứ giác ABDC.
d) Giả sử H là trung điểm của AM. Chứng minh diện tích của tam giác ABC bằng diện tích của tứ giác BHCD.
Bài tập 20 trang 95 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho hình bình hành ABCD có $\widehat{A}$ > 90°, AB > BC. Trên đường thẳng vuông góc với BC tại C lấy hai điểm E, F sao cho CE = CF = BC. Trên đường thẳng vuông góc với CD tại C lấy hai điểm P, Q sao cho CP = CQ = CD (Hình 16). Chứng minh:
a) Tứ giác EPFQ là hình bình hành;
b*) AC ⊥ EP.
90°, AB > BC. Trên đường thẳng vuông góc với BC tại C lấy hai điểm E, F sao cho CE = CF = BC. Trên đường thẳng vuông góc với CD tại C lấy hai điểm P, Q sao cho CP = CQ = CD (Hình 16). Chứng minh: a) Tứ giác EPFQ là hình bình hành; b*) AC ⊥ EP." width="260" height="373">