Giải bài tập sách bài tập (SBT) toán lớp 8 Cánh diều bài 6 Hình thoi
Giải bài tập sách bài tập toán lớp 8 Cánh diều bài 6: Hình thoi
Trong bài viết này, chúng ta sẽ tìm hiểu cách giải chi tiết bài tập về hình thoi trong sách bài tập toán lớp 8 Cánh diều. Sytu sẽ hướng dẫn một cách chi tiết và dễ hiểu nhất để các bạn học sinh có thể nắm vững kiến thức và làm bài tập một cách hiệu quả. Hy vọng rằng thông qua bài viết này, các bạn sẽ cảm thấy tự tin và hiểu biết hơn trong việc giải các bài toán liên quan đến hình thoi.
Bài tập và hướng dẫn giải
Bài tập 26 trang 99 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho hình thoi ABCD có góc B tù. Kẻ BE vuông góc AD tại E, BF vuông góc với CD tại F. Gọi M, N lần lượt là giao điểm của BE, BF với AC. Chứng minh tứ giác BMDN là hình thoi.
Bài tập 27 trang 99 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho một hình thoi có độ dài hai đường chéo là $\frac{18}{5}$ m và $\frac{27}{10}$ m. Tính chu vi và diện tích của hình thoi đó.
Bài tập 28 trang 100 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho tam giác ABC nhọn có các đường cao BD, CE. Tia phân giác của các góc ACE, ABD cắt nhau tại O và cắt AB, AC lần lượt tại M, N. Tia BN cắt CE tại K, tia CM cắt BD tại H. Chứng minh:
a) BN ⊥ CM;
b) Tứ giác MNHK là hình thoi.
Bài tập 29 trang 100 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
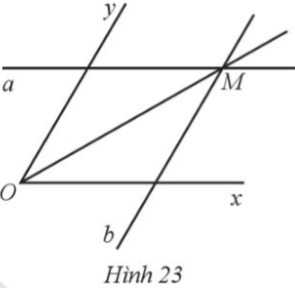
Cho góc xOy khác góc bẹt. Dùng thước hai lề (thước có hai cạnh song song). Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Ox của góc xOy, vẽ đường thẳng a theo cạnh kia của thước. Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Oy của góc xOy, vẽ đường thẳng b theo cạnh kia của thước. Hai đường thẳng a, b cắt nhau tại điểm M nằm trong góc xOy (Hình 23). Chứng minh tia OM là tia phân giác của góc xOy.
Bài tập 30 trang 100 sách bài tập (SBT) toán lớp 8 tập 1 cánh diều:
Cho hình thoi ABCD có AB = 2 cm, $\widehat{A}=\frac{1}{2}\widehat{B}$. Các điểm H, K thay đổi lần lượt trên cạnh AD, CD sao cho $\widehat{HBK}$ = 60°.
a) Chứng minh DH + DK không đổi.
b) Xác định vị trí của các điểm H, K để độ dài HK ngắn nhất. Tính độ dài ngắn nhất đó.





