Giải bài tập 3: Hình cầu Diện tích mặt cầu và thể tích hình cầu
Hình cầu và các khái niệm liên quan
Hình cầu là một kiểu hình học trong đó một hình tròn quay quanh đường kính của nó để tạo ra một hình cầu. Hình cầu được xác định bởi tâm $O$ và bán kính $R$.
Mỗi hình cầu có diện tích mặt cầu và thể tích riêng biệt. Diện tích mặt cầu được tính theo công thức $S = 4 \pi R^{2}$ hoặc $S = \pi d^{2}$, với $R$ là bán kính và $d$ là đường kính mặt cầu.
Thể tích hình cầu được tính bằng công thức $V = \frac{4}{3} \pi R^{3}$, trong đó $R$ là bán kính của hình cầu. Đây là khái niệm quan trọng giúp chúng ta hiểu rõ về không gian và hình dạng của các vật thể tròn.
Chúng ta có thể áp dụng kiến thức về hình cầu vào thực tế, như việc tính toán diện tích bề mặt của một quả cầu hoặc thể tích của một quả cầu để giải quyết các bài toán trong cuộc sống hàng ngày.
Bài tập và hướng dẫn giải
Câu 30: Trang 124 - sách giáo khoa (SGK) toán lớp 9 tập 2
Nếu thể tích của một hình cầu là $113\frac{1}{7}cm^{3}$ thì trong các kết quả sau đây, kết quả nào là bán kính của nó (lấy $\pi \approx \frac{22}{7}$)
(A) 2 cm (B) 3 cm (C) 5 cm (D) 6 cm (E) Một kết quả khác
Câu 31: Trang 124 - sách giáo khoa (SGK) toán lớp 9 tập 2
Hãy điền vào các ô trống ở bảng sau:
Câu 32: Trang 125 - sách giáo khoa (SGK) toán lớp 9 tập 2
Một khối gỗ dạng hình trụ, bán kính đường tròn là \(r\), chiều cao \(2r\) (đơn vị: cm)
Người ta khoét rỗng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại(diện tích cả ngoài lẫn trong).
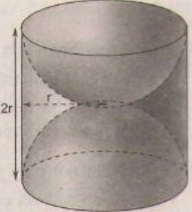
Hình 108
Câu 33: Trang 125 - sách giáo khoa (SGK) toán lớp 9 tập 2
Dụng cụ thể thao.
Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau(làm tròn kết quả đến chữ số thập phân thứ hai):
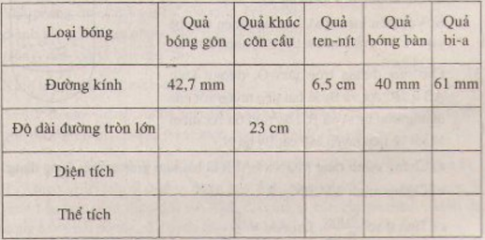
Câu 34: Trang 125 - sách giáo khoa (SGK) toán lớp 9 tập 2
Khinh khí cầu của nhà Mông-gôn-fi-ê (Montgolfier)
Ngày 4 - 6 - 1783, anh em nhà Mông-gôn-fi-ê (người Pháp) phát minh ra khinh khí cầu dùng không khí nóng. Coi khí cầu này là hình cầu có đường kính $11m$. Hãy tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến chữ số thập phân thứ hai).
Hình 109
Câu 35: Trang 126 - sách giáo khoa (SGK) toán lớp 9 tập 2
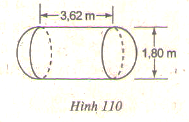
Một cái bồn chứa xăng gồm hai cửa hình cầu và hình trụ (h110)
Hãy tính thể tích của bồn chưa theo kích thước cho trên hình vẽ.
Câu 36: Trang 126 - sách giáo khoa (SGK) toán lớp 9 tập 2
Một chi tiết máy gồm một hình trù và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm)
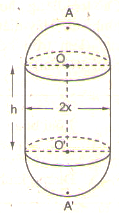
Hình 111
a) Tìm một hệ thức giữa \(x\) và \(h\) khi \(AA'\) có độ dài không đổi và bằng \(2a\).
b) Với điều kiện ở a) hãy tính diện tích bề mặt và thể tích của chi tiết theo \(x\) và \(a\).
Câu 37: Trang 126 - sách giáo khoa (SGK) toán lớp 9 tập 2
Cho nửa đường tròn tâm \(O\), đường kính \(AB = 2R\), \(Ax\) và \(By\) là hai tiếp tuyến với nửa đường tròn tại \(A\) và \(B\). Lấy trên tia \(Ax\) điểm \(M\) rồi vẽ tiếp tuyến \(MP\) cắt \(By\) tại \(N\).
a) Chứng minh rằng \(MON\) và \(APB\) là hai tam giác vuông đồng dạng.
b) Chứng minh rằng \(AM.BN = R^2\)
c) Tính tỉ số \(\frac{S_{MON}}{S_{APB}}\)khi \(AM\) = \(\frac{R}{2}\)
d) Tính thể tích của hình do nửa hình tròn \(APB\) quay quanh \(AB\) sinh ra.