Giải bài tập 7: Tứ giác nội tiếp
Tứ giác nội tiếp: Sự kỳ diệu của đường tròn
Đường tròn không chỉ xuất hiện trong tam giác mà còn có thể xuất hiện trong tứ giác. Điều đó có nghĩa là chúng ta luôn có thể vẽ được một đường tròn đi qua bốn đỉnh của một tứ giác. Điều này chứng tỏ sức mạnh và sự linh hoạt của hình học, đồng thời mở ra những khám phá mới hơn về tứ giác nội tiếp.
Bài học về tứ giác nội tiếp giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của tứ giác khi đặt trên đường tròn. Trong sách giáo khoa Toán lớp 9 tập 2, chúng ta sẽ được học và thực hành giải các bài tập liên quan đến tứ giác nội tiếp một cách chi tiết và dễ hiểu nhờ sự hướng dẫn của Sytu.
Thông qua việc tóm tắt lý thuyết về tứ giác nội tiếp, chúng ta có thể nắm vững những định nghĩa, định lí cơ bản như: một tứ giác nội tiếp đường tròn là tứ giác có bốn đỉnh nằm trên một đường tròn; trong tứ giác nội tiếp, tổng số đo hai góc đối diện bằng $180^{\circ}$...
Hy vọng rằng, với tài liệu hữu ích này, các em học sinh sẽ có thêm kiến thức và kỹ năng trong việc giải các bài toán liên quan đến tứ giác nội tiếp, từ đó nâng cao hiểu biết và tự tin khi học môn Toán.
Bài tập và hướng dẫn giải
Câu 53: Trang 89 - sách giáo khoa (SGK) toán lớp 9 tập 2
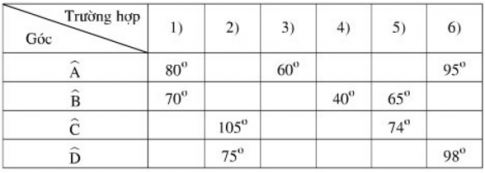
Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bảng sau (nếu có thể):
Câu 54: Trang 89 - sách giáo khoa (SGK) toán lớp 9 tập 2
Tứ giác ABCD có $\widehat{ABC}+\widehat{ADC}=180^{\circ}$.
Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm
Câu 55: Trang 89 - sách giáo khoa (SGK) toán lớp 9 tập 2
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết $\widehat{DAB}=80^{\circ}$, $\widehat{DAM}=30^{\circ}$, $\widehat{BMC}=70^{\circ}$. Hãy tính số đo các góc $\widehat{MAB}$, $\widehat{BCM}$, $\widehat{AMB}$, $\widehat{DMC}$, $\widehat{AMD}$, $\widehat{MCD}$ và $\widehat{BCD}$.
Câu 56: Trang 89 - sách giáo khoa (SGK) toán lớp 9 tập 2
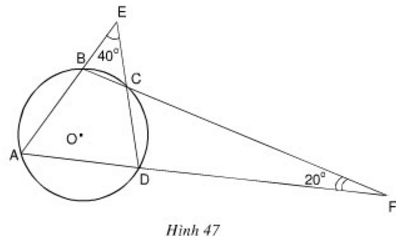
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
Câu 57: Trang 89 - sách giáo khoa (SGK) toán lớp 9 tập 2
Trong các hình sau, hình nào nội tiếp được trong một đường tròn:
Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân? Vì sao?
Câu 58: Trang 90 - sách giáo khoa (SGK) toán lớp 9 tập 2
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho
DB = DC, $\widehat{DCB}=\frac{1}{2}.\widehat{ACB}$
a) Chứng minh ABCD là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm A, B, C, D.
Câu 59: Trang 90 - sách giáo khoa (SGK) toán lớp 9 tập 2
Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.
Câu 60: Trang 90 - sách giáo khoa (SGK) toán lớp 9 tập 2
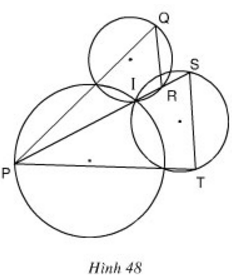
Xem hình 48. Chứng minh QR // ST.
Hướng dẫn: Xét cặp góc so le trong $\widehat{PST},\widehat{SRQ}$