Giải bài tập 4: Góc tạo bởi tia tiếp tuyến và dây cung
Góc tạo bởi tia tiếp tuyến và dây cung
Bài học này sẽ giúp bạn hiểu rõ về khái niệm về góc tạo bởi tia tiếp tuyến và dây cung trên đường tròn. Đầu tiên, góc tạo bởi tia tiếp tuyến và dây cung được định nghĩa là góc $\widehat{BAx}$ trong đó $A$ là đỉnh của góc nằm trên đường tròn, tia $Ax$ là tia tiếp tuyến và cạnh còn lại (cạnh chứa dây cung $AB$).
Một điểm quan trọng khác đó là số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn. Điều này giúp chúng ta có thể tính toán góc một cách chính xác và dễ dàng hơn.
Ngoài ra, trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung cũng bằng góc nội tiếp cùng chắn một cung. Điều này cũng là một điểm quan trọng giúp ta hiểu rõ hơn về mối quan hệ giữa các góc trên đường tròn.
Hy vọng rằng bài học này sẽ giúp bạn hiểu rõ và áp dụng thành thạo hơn trong việc giải các bài tập liên quan đến góc tạo bởi tia tiếp tuyến và dây cung trên đường tròn.
Bài tập và hướng dẫn giải
Câu 27: Trang 79 – sách giáo khoa (SGK) toán lớp 9 tập 2
Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh $\widehat{APO}$ = $\widehat{PBT}$
Câu 28: Trang 79 – sách giáo khoa (SGK) toán lớp 9 tập 2
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).
Câu 29: Trang 79 – sách giáo khoa (SGK) toán lớp 9 tập 2
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D. Chứng minh: $\widehat{CBA}$ = $\widehat{DBA}$
Câu 30: Trang 79 – sách giáo khoa (SGK) toán lớp 9 tập 2
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung, cụ thể là: Nếu $\widehat{BAx}$ (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB) có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
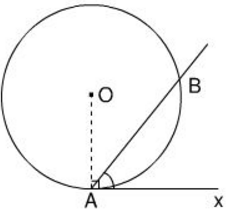
H. 29
Câu 31: Trang 79 – sách giáo khoa (SGK) toán lớp 9 tập 2
Cho đường tròn (O; R) và dây cung BC = R . Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính $\widehat{ABC}$ và $\widehat{BAC}$
Câu 32: Trang 80 – sách giáo khoa (SGK) toán lớp 9 tập 2
Cho đường tròn tâm O đường kính AB. Một tiếp tuyến của đường tròn tại P cắt đường thẳng AB tại T (điểm B nằm giữa O và T).
Chứng minh rằng: $\widehat{BTP}$ + $2$ . $\widehat{TPB}$ = $90^{\circ}$
Câu 33: Trang 80 – sách giáo khoa (SGK) toán lớp 9 tập 2
Cho A, B, C là ba điểm trên một đường tròn, At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh AB.AM = AC.AN.
Câu 34: Trang 80 – sách giáo khoa (SGK) toán lớp 9 tập 2
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.
Chứng minh $MT^{2}$ = $MA.MB$
Câu 35: Trang 80 – sách giáo khoa (SGK) toán lớp 9 tập 2
Trên bờ biển có một ngọn hải đăng cao 40m. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trong thấy ngọn đèn này, biết rằng mắt người quan sát ở độ cao 10m so với mực nước biển và bán kính Trái Đất gần bằng 6400km (h.30)?
Hướng dẫn: Áp dụng kết quả của bài tập 34.
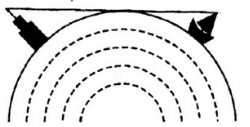
H. 30