Bài tập 4.8 trang 50 sách bài tập (SBT) toán lớp 8 tập 1 kết nối:Cho tam giác DEF. Gọi H, K, I lần...
Câu hỏi:
Bài tập 4.8 trang 50 sách bài tập (SBT) toán lớp 8 tập 1 kết nối:
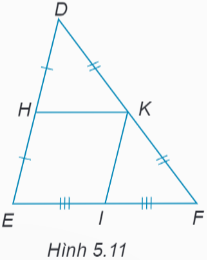
Cho tam giác DEF. Gọi H, K, I lần lượt là các trung điểm của DE, DF và EF. Chứng minh rằng tứ giác HKIE là hình bình hành.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Ngọc
Để chứng minh rằng tứ giác HKIE là hình bình hành, ta sẽ thực hiện theo các bước sau:**Bước 1:** Chứng minh rằng HK = EIVì H là trung điểm của DE, K là trung điểm của DF, nên ta có:- HK là đường trung bình của tam giác DEF, nên HK = 1/2 EF (tính chất đường trung bình của tam giác)- I là trung điểm của EF, nên EI = 1/2 EFDo đó, ta có HK = EI**Bước 2:** Chứng minh rằng HK // EIVì HK là đường trung bình của tam giác DEF và I là trung điểm của EF, nên ta có HK // EF. Vậy tứ giác HKIE có 2 cạnh đối nhau bằng nhau và hai cạnh còn lại song song, từ đó suy ra tứ giác HKIE là hình bình hành.Vậy ta đã chứng minh rằng tứ giác HKIE là hình bình hành.
Câu hỏi liên quan:
- Bài tập 4.7 trang 50 sách bài tập (SBT) toán lớp 8 tập 1 kết nối:Tìm độ dài x, y trong hình vẽ...
- Bài tập 4.9 trang 50 sách bài tập (SBT) toán lớp 8 tập 1 kết nối:Cho tam giác ABC, các đường trung...
- Bài tập 4.10 trang 50 sách bài tập (SBT) toán lớp 8 tập 1 kết nối:Cho hình chữ nhật ABCD. Gọi D, E,...
Bình luận (0)




