Bài tập 10. Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD 6.a)...
Câu hỏi:
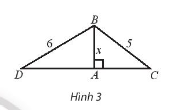
Bài tập 10. Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD 6.
a) Biểu diễn độ đài cạnh AC và AD theo x.
b) Tìm x để chu vi của tam giác ABC là 12.
c) Tìm x để AD = 2AC.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Đạt
Phương pháp giải:
a) Ta sử dụng định lý Pythagore trong tam giác vuông để tính độ dài cạnh AC và cạnh AD:
AC = √(BC^2 - AB^2) = √(5^2 - x^2) = √(25 - x^2)
AD = √(BD^2 - AB^2) = √(6^2 - x^2) = √(36 - x^2)
b) Chu vi của tam giác ABC là tổng độ dài 3 cạnh:
AB + AC + BC = 12
x + 5 + √(25 -x^2) = 12
Suy ra, x = 3 hoặc x = 4
c) Ta cần tìm giá trị x để AD = 2AC:
√(36 - x^2) = 2√(25 - x^2)
36 - x^2 = 4(25 - x^2)
36 - x^2 = 100 - 4x^2
3x^2 = 64
x^2 = 64/3
x = ± 8√3 / 3
Vì x > 0, nên x = 8√3 / 3.
Vậy, câu trả lời đầy đủ và chi tiết hơn là:
a) AC = √(25 - x^2), AD = √(36 - x^2)
b) x = 3 hoặc x = 4
c) x = 8√3 / 3.
a) Ta sử dụng định lý Pythagore trong tam giác vuông để tính độ dài cạnh AC và cạnh AD:
AC = √(BC^2 - AB^2) = √(5^2 - x^2) = √(25 - x^2)
AD = √(BD^2 - AB^2) = √(6^2 - x^2) = √(36 - x^2)
b) Chu vi của tam giác ABC là tổng độ dài 3 cạnh:
AB + AC + BC = 12
x + 5 + √(25 -x^2) = 12
Suy ra, x = 3 hoặc x = 4
c) Ta cần tìm giá trị x để AD = 2AC:
√(36 - x^2) = 2√(25 - x^2)
36 - x^2 = 4(25 - x^2)
36 - x^2 = 100 - 4x^2
3x^2 = 64
x^2 = 64/3
x = ± 8√3 / 3
Vì x > 0, nên x = 8√3 / 3.
Vậy, câu trả lời đầy đủ và chi tiết hơn là:
a) AC = √(25 - x^2), AD = √(36 - x^2)
b) x = 3 hoặc x = 4
c) x = 8√3 / 3.
Câu hỏi liên quan:
- A. Trắc nghiệmBài tập 1. Tam thức bậc hai nào có biệt thức $\Delta = 1$ và hai nghiệm là: $x_{1}...
- Bài tập2. Tam thức bậc hai nào đương với mọi x $\in \mathbb{R}$?A. $2x^{2} - 4x + 2$;...
- Bài tập 3. Khẳng định nào sau đây đúng với tam thức bậc hai ƒ(x) = $10x^{2} - 3x - 4$?A. f(x) > ...
- Bài tập4. Trong trường hợp nào tam thức bậc hai f(x) = $ax^{2} + bx + c$ có $\Delta$ > 0...
- Bài tập 5. Cho đồ thị của hàm số bậc hai y = f(x) như Hình 1. Tập nghiệm của bất phương trình ƒ(x)...
- Bài tập6. Bất phương trình nào có tập nghiệm là (2; 5)?A. $x^{2} - 7x + 10 > 0$;...
- Bài tập 7. Tập xác định của hàm số $y =\frac{1}{\sqrt{9x^{2} - 3x - 2}} + \sqrt{3 - x}$ là:A....
- Bài tập 8. Với giá trị nào của tham số m thì phương trình $(2m + 6)^{2} + 4mx + 3 = 0$ có hai...
- Bài tập9. Giá trị nào là nghiệm của phương trình $\sqrt{x^{2} + x + 11} = \sqrt{-2x^{2} - 13x...
- Bài tập 10. Khẳng định nào đúng với phương trình $\sqrt{2x^{2} - 3x - 1} = \sqrt{3x^{2} - 2x - 13}$...
- Bài tập 11. Khẳng định nào đúng với phương trình $\sqrt{5x^{2} + 27x + 36} = 2x + 5$ ?A. Phương...
- Bài tập 12. Cho đồ thị của hai hàm sô bậc hai f(x) = $ax^{2} + bx + c$ và g(x) = $dx^{2} + ex + h$...
- B. Tự luậnBài tập 1. Dựa vào đồ thị của hàm số bậc hai y = f(x) sau đây, hãy xét dấu của tam thức...
- Bài tập2. Xét dấu của các tam thức bậc hai sau:a) f(x) = $-7x^{2} + 44x - 45$; ...
- Bài tập 3. Giải các bất phương trình bậc hai sau:a) $x^{2} - 10x + 24\geq 0$; ...
- Bài tập 4. Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:
- Bài tập 5.Giải các phương trình sau:a) $\sqrt{3x^{2} + 7x - 1} = \sqrt{6x^{2} + 6x -...
- Bài tập6. Tìm tập xác định của các hàm số sau:a) y = $\sqrt{-x^{2} + 6x - 2}$; ...
- Bài tập 7. Tìm các giá trị của tham số m để:a) f(x) = $(m - 3)^{2} + 2mx - m$ là một tam thức bậc...
- Bài tập 8. Người la thử nghiệm ném một quả bóng trên Mặt Trăng. Nếu quả bóng được ném lên từ độ cao...
- Bài tập 9. Mội người phát cầu qua lưới từ độ cao $y_{o}$ mét, nghiêng mội góc $\alpha$ so với...
Bình luận (0)





