Bài tập 5.6 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho tam giác vuông ABC vuông tại...
Câu hỏi:
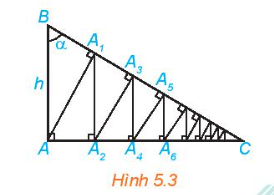
Bài tập 5.6 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng $\alpha $ (H.5.3). Từ A kẻ $AA_{1}\perp BC$, từ $A_{1}$ kẻ $A_{1}A_{2}\perp AC$, sau đó lại kẻ $A_{2}A_{3}\perp BC$. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA_{1}A_{2}A_{3}... Tính độ dài đường gấp khúc này theo h và $\alpha $
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Linh
Để tính độ dài của đường gấp khúc $AA_{1}A_{2}A_{3}...$, ta sẽ sử dụng công thức tổng của cấp số nhân với số hạng tổng quát là $u_{n}=sin\alpha \times h\times (sin\alpha )^{n-1}$.Đầu tiên, ta tính $AA_{1}$:Vì $A_{1}A\perp BC$ và tam giác $ABC$ vuông tại $A$, nên ta có $\frac{AA_{1}}{AB} = sin\alpha$.Do đó, $AA_{1} = AB \times sin\alpha = h \times sin\alpha$.Tiếp theo, ta tính $A_{2}A_{3}$:Tương tự như trên, ta có $\frac{A_{2}A_{3}}{A_{1}A_{2}} = sin\alpha$.Vì tam giác $AA_{1}A_{2}$ vuông tại $A_{1}$, nên $A_{1}A_{2} = AA_{1} = h \times sin\alpha$.Do đó, $A_{2}A_{3} = A_{1}A_{2} \times sin\alpha = h \times (sin\alpha)^{2}$.Cứ tiếp tục như vậy, ta sẽ thấy rằng $A_{n}A_{n+1} = h \times (sin\alpha)^{n}$.Vậy, tổng độ dài của đường gấp khúc $AA_{1}A_{2}A_{3}...$ là:$AA_{1} + A_{2}A_{3} + ... = h \times sin\alpha + h \times (sin\alpha)^{2} + h \times (sin\alpha)^{3} + ... $$= h \times sin\alpha(1 + (sin\alpha) + (sin\alpha)^{2} + ...)$Đây là tổng của cấp số nhân vô hạn với $u_{1} = h \times sin\alpha$, $q = sin\alpha$.Vậy, ta có:$AA_{1} + A_{2}A_{3} + ... = \frac{h \times sin\alpha}{1 - sin\alpha}$.Vậy, độ dài của đường gấp khúc được tạo thành là $\frac{h \times sin\alpha}{1 - sin\alpha}$.
Câu hỏi liên quan:
- 1. Giới hạn hữu hạn của dãy sốHoạt động 1 trang 105 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:...
- Luyện tập 1 trang 105 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Chứng minh rằng...
- Hoạt động 2 trang 105 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Nhận biết dãy số có giới hạn hữu...
- Luyện tập 2 trang 106 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho dãy số $(u_{n})$ với...
- Vận dụng 1 trang 106 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Một quả bóng cao su được thả từ...
- 2. Định lí về giới hạn của dãy sốHoạt động 3 trang 106 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:...
- Luyện tập 3 trang 107 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tìm $\underset{n\rightarrow...
- 3. Tổng của cấp số nhân lùi vô hạnHoạt động 4 trang 107 sách giáo khoa (SGK) toán lớp 11 tập 1...
- Luyện tập 4 trang 108 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tính tổng...
- Vận dụng 2 trang 108 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: (Giải thích nghịch lí Zeno)Để đơn...
- 4. Giới hạn vô cực của dãy sốHoạt động 5 trang 108 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:...
- Luyện tập 5 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính $\underset{n\rightarrow...
- Bài tậpBài tập 5.1 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tìm các giới hạn sau:a)...
- Bài tập 5.2 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hai dãy số không âm...
- Bài tập 5.3 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tìm giới hạn của các dãy số cho...
- Bài tập 5.4 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Viết các số thập phân vô hạn...
- Bài tập 5.5 trang 109 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Một bệnh nhân hàng ngày phải...
Bình luận (0)





