Giải bài tập toán lớp 11 kết nối tri thức bài 16 Giới hạn của hàm số
Bài toán GiảI hàm số lớp 11: Xác định giới hạn của hàm số trong sách toán lớp 11 tập 1 kết nối tri thức
Trong bài toán giải hàm số số 16, chúng ta sẽ tìm hiểu và áp dụng kiến thức về giới hạn của hàm số. Đây là một phần quan trọng trong chương trình học của sách giáo khoa toán học. Chúng ta sẽ được cung cấp phần đáp án chuẩn kèm theo hướng dẫn giải chi tiết từng bài tập, nhằm giúp các em học sinh hiểu rõ và nắm vững kiến thức được trình bày.
Hãy cùng tìm hiểu và giải quyết các bài tập trong phần này để nâng cao kiến thức và kỹ năng giải toán của mình. Chúng ta cùng nhau vượt qua mỗi bước thách thức và phát triển khả năng tư duy logic, suy luận trong việc giải quyết các bài toán toán học.
Hy vọng rằng, sau khi học xong phần này, các em sẽ tự tin hơn và có khả năng áp dụng kiến thức vào thực tế một cách linh hoạt hơn.
Bài tập và hướng dẫn giải
1. Giới hạn hữu hạn của hàm số tại một điểm
Hoạt động 1 trang 111 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Nhận biết khái niệm giới hạn tại một điểm
Cho hàm số $f(x)=\frac{4-x^{2}}{x-2}$
a) Tìm tập xác định của hàm số f(x)
b) Cho dãy số $x_{n}=\frac{2n+1}{n}$. Rút gọn $f(x_{n})$ và tính giới hạn của dãy $(u_{n})$ với $u_{n}=f(x_{n})$
c) Với dãy số $(x_{n})$ bất kì sao cho $x_{n}\neq 2$ và $x_{n}\rightarrow 2$, tính $f(x_{n})$ và tìm $\underset{n\rightarrow +\infty }{lim}f(x_{n})$
Luyện tập 1 trang 113 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính $\underset{n\rightarrow 1 }{lim}\frac{x-1}{\sqrt{x}-1}$
Hoạt động 2 trang 113 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Nhận biết khái niệm giới hạn một bên
Cho hàm số $f(x)=\frac{|x-1|}{x-1}$
a) Cho $x_{n}=\frac{n}{n+1}$ và $x'_{n}=\frac{n+1}{n}$. Tính $y_{n}=f(x_{n})$ và $y'_{n}=f(x'_{n})$
b) Tìm giới hạn của các dãy số $(y_{n})$ và $(y'_{n})$
c) Cho các dãy số $(x_{n})$ và $(x'_{n})$ bất kì sao cho $x_{n}<1<x'_{n}$ và $x_{n}\rightarrow 1,x'_{n}\rightarrow 1$, tính $\underset{n\rightarrow +\infty }{lim}f(x_{n})$ và $\underset{n\rightarrow +\infty }{lim}f(x'_{n})$
Luyện tập 2 trang 113 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hàm số $f(x)=\left\{\begin{matrix}-x nếu x<0\\ \sqrt{x}nếu x\geq 0\end{matrix}\right.$
Tính $\underset{x\rightarrow 0^{+}}{lim}f(x), \underset{x\rightarrow 0^{-}}{lim}f(x)$ và $\underset{x\rightarrow 0}{lim}f(x)$
2. Giới hạn hữu hạn của hàm số tại vô cực
Hoạt động 3 trang 114 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Nhận biết khái niệm giới hạn tại vô cực
Cho hàm số $f(x)=1+\frac{2}{x-1}$ có đồ thị như Hình 5.4
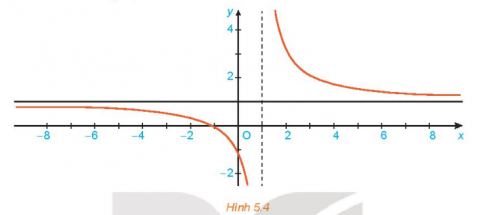
Giả sử $(x_{n})$ là dãy số sao cho $x_{n}>1,x_{n}\rightarrow +\infty $. Tính $f(x_{n})$ và tìm $\underset{n\rightarrow +\infty }{lim}f(x_{n})$
Luyện tập 3 trang 115 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính $\underset{x\rightarrow +\infty }{lim}\frac{\sqrt{x^{2}+2}}{x+1}$
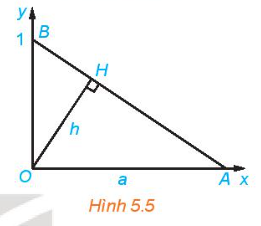
Vận dụng trang 115 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho tam giác vuông OAB với A = (a;0) và B = (0;1) như Hình 5.5. Đường cao OH có độ dài là h
a) Tính h theo a
b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?
3. Giới hạn vô cực của hàm số tại một điểm
Hoạt động 4 trang 115 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Nhận biết khái niệm giới hạn vô cực
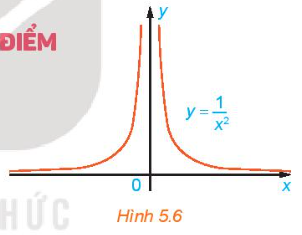
Xét hàm số $f(x)=\frac{1}{x^{2}}$ có đồ thị như Hình 5.6
Cho $x_{n}=\frac{1}{n}$, chứng tỏ rằng $f(x_{n})\rightarrow +\infty $
Hoạt động 5 trang 116 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hàm số $f(x)=\frac{1}{x-1}$. Với các dãy số $(x_{n})$ và $(x'_{n})$ cho bởi $x_{n}=1+\frac{1}{n},x'_{n}=1-\frac{1}{n}$, tính $\underset{x\rightarrow +\infty }{lim}f(x_{n})$ và $\underset{x\rightarrow +\infty }{lim}f(x'_{n})$
Luyện tập 4 trang 116 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính các giới hạn
a) $\underset{x\rightarrow 0}{lim}\frac{2}{|x|}$
b) $\underset{x\rightarrow 2^{-} }{lim}\frac{1}{\sqrt{2-x}}$
Luyện tập 5 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính $\underset{x\rightarrow 2^{+}}{lim}\frac{2x-1}{x-2}$ và $\underset{x\rightarrow 2^{-}}{lim}\frac{2x-1}{x-2}$
Bài tập
Bài tập 5.7 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hai hàm số $f(x)=\frac{x^{2}-1}{x-1}$ và g(x) = x + 1. Khẳng định nào sau đây là đúng?
a) f(x) = g(x)
b) $\underset{x\rightarrow 1}{lim}f(x)=\underset{x\rightarrow 1}{lim}g(x)$
Bài tập 5.8 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính các giới hạn sau:
a) $\underset{x\rightarrow 0}{lim}\frac{(x+2)^{2}-4}{x}$
b) $\underset{x\rightarrow 0}{lim}\frac{\sqrt{x^{2}+9}-3}{x^{2}}$
Bài tập 5.9 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hàm số $H(t)=\left\{\begin{matrix}0 nếu t<0\\ 1 nếu t\geq 0\end{matrix}\right.$ (hàm Heaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/ mở của dòng điện tại thời điểm t = 0)
Tính $\underset{t\rightarrow 0^{+}}{lim}H(t)$ và $\underset{t\rightarrow 0^{-}}{lim}H(t)$
Bài tập 5.10 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính các giới hạn một bên:
a) $\underset{t\rightarrow 1^{+}}{lim}\frac{x-2}{x-1}$
b) $\underset{t\rightarrow 4^{-}}{lim}\frac{x^{2}-x+1}{4-x}$
Bài tập 5.11 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hàm số $g(x)=\frac{x^{2}-5x+6}{|x-2|}$
Tìm $\underset{t\rightarrow 2^{+}}{lim}g(x)$ và $\underset{t\rightarrow 2^{-}}{lim}g(x)$
Bài tập 5.12 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tính các giới hạn sau:
a) $\underset{x\rightarrow +\infty }{lim}\frac{1-2x}{\sqrt{x^{2}+1}}$
b) $\underset{x\rightarrow +\infty }{lim}(\sqrt{x^{2}+x+2}-x)$
Bài tập 5.13 trang 118 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hàm số $f(x)=\frac{2}{(x-1)(x-2)}$
Tìm $\underset{x\rightarrow 2^{+} }{lim}f(x)$ và $\underset{x\rightarrow 2^{-} }{lim}f(x)$





