Giải bài tập toán lớp 11 kết nối tri thức bài Bài tập cuối chương II
Giải bài tập toán lớp 11 và kết nối tri thức
Bạn có đang gặp khó khăn với việc giải bài tập toán lớp 11? Hãy tham khảo sách Giải bài tập toán lớp 11 kết nối tri thức để có phần đáp án chuẩn và hướng dẫn giải chi tiết cho từng bài tập trong chương trình học. Qua đó, bạn sẽ có cơ hội nắm vững kiến thức và hiểu rõ hơn về bài tập cuối chương II. Hy vọng rằng, thông qua sách giáo khoa này, các em học sinh sẽ có một cách tiếp cận mới, dễ hiểu và phong phú hơn với môn toán, giúp họ phát triển tư duy logic và khả năng giải quyết vấn đề.
Bài tập và hướng dẫn giải
A - Trắc nghiệm
Bài tập 2.22 trang 56 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Khẳng định nào sau đây là sai?
A. Một dãy số tăng thì bị chặn dưới
B. Một dãy số giảm thì bị chặn trên
C. Một dãy số bị chặn thì phải tăng hoặc giảm
D. Một dãy số không đổi thì bị chặn
Bài tập 2.23 trang 56 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho dãy số $1,\frac{1}{2},\frac{1}{4},\frac{1}{8},...$ (số hạng sau bằng một nửa số hạng liền trước nó)
Công thức tổng quát của dãy số đã cho là:
A. $u_{n}=(\frac{1}{2})^{n}$
B. $u_{n}=\frac{(-1)^{n}}{2^{n-1}}$
C. $u_{n}=\frac{1}{2n}$
D. $u_{n}=(\frac{1}{2})^{n-1}$
Bài tập 2.24 trang 56 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho dãy số $(u_{n})$ với $u_{n}=3n+6$. Khẳng định nào sau đây là đúng?
A. Dãy số $(u_{n)$ là cấp số cộng với công sai d = 3
B. Dãy số $(u_{n)$ là cấp số cộng với công sai d = 6
C. Dãy số $(u_{n)$ là cấp số nhân với công bội q = 3
D. Dãy số $(u_{n)$ là cấp số nhân với công bội q = 6
Bài tập 2.25 trang 56 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Trong dãy số cho bởi công thức truy hồi sau, dãy số nào là cấp số nhân?
A. $u_{1}=-1,u_{n+1}=u_{n}^{2}$
B. $u_{1}=-1,u_{n+1}=2u_{n}$
C. $u_{1}=-1,u_{n+1}=u_{n}+2$
D. $u_{1}-1,u_{n+1}=u_{n}-2$
Bài tập 2.26 trang 56 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tổng 100 số hạng đầu của dãy số ($u_{n}$) với $u_{n}=2n-1$ là
A. 199
B. $2^{100}-1$
C. 10000
D. 9999
B - Tự luận
Bài tập 2.27 trang 57 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Từ 0 giờ đến 12 giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu tiếng, biết rằng nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?
Bài tập 2.28 trang 57 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi sau 24 giờ, tế bao ban đầu sẽ phân chia thành bao nhiêu tế bào?
Bài tập 2.29 trang 57 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Chứng minh rằng:
a) Trong một cấp số cộng $(u_{n})$, mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu có) đều là số trung bình cộng của hai số hạng đứng kề với nó, nghĩa là $u_{k}=\frac{u_{k-1}+u_{k+1}}{2}$ với $k\geq 2$
b) Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu có) đều là tích của hai số hạng đứng kề nó, nghĩa là $u_{k}^{2}=u_{k-1}\times u_{k-1}$ với $k\geq 2$
Bài tập 2.30 trang 57 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tìm ba số, biết theo thứ tự đó chúng lập thành cấp số cộng và có tổng bằng 21, và nếu lần lượt cộng thêm các số 2; 3; 9 vào ba số đó thì được ba số lập thành một cấp số nhân.
Bài tập 2.31 trang 57 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Mặt sàn tầng một (tầng trệt) của một ngôi nhà cao hơn mặt sân 0.5 m. Cầu thang đi từ tầng một lên tầng hai gồm 25 bậc, mỗi bậc cao 16 cm.
a) Viết công thức để tìm độ cao của bậc cầu thang thứ n so với mặt sân
b) Tính độ cao của sàn tầng hai so với mặt sân
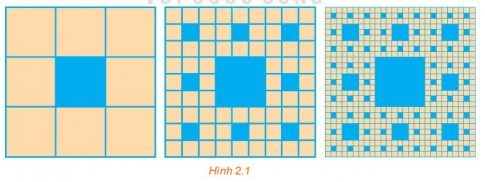
Bài tập 2.32 trang 57 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con và mỗi hình vuông con ở chính giữa lại được tô màu xanh. Nếu quá trình này tiếp tục lặp lại năm lần, thì tổng diện tích các hình vuông được tô màu xanh là bao nhiêu?
