Giải bài tập toán lớp 11 kết nối tri thức bài 17 Hàm số liên tục

1. Hàm số liên tục tại một điểm

Hoạt động 1 trang 119 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Nhận biết tính liên tục của hàm số tại một điểm

Cho hàm số $f(x)=\left\{\begin{matrix}\frac{x^{2}-1}{x-1} nếu x\neq 1\\2 nếu x = 1 \end{matrix}\right.$

Tính giới hạn $\underset{x\rightarrow 1}{lim}f(x)$ và so sánh giá trị này với f(1)

Luyện tập 1 trang 120 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Xét tính liên tục của hàm số $f(x)=\begin{Bmatrix}-x nếu x<0\\ 0 nếu x =0 \\ x^{2} nếu x >0 \end{Bmatrix}$ tại điểm $x_{0}=0$

2. Hàm số liên tục trên một khoảng

Hoạt động 2 trang 120 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hai hàm số $f(x)=\left\{\begin{matrix}2x nếu 0\leq x\frac{1}{2}\\ 1 nếu \frac{1}{2}<x\leq 1 \end{matrix}\right.$ và $g(x)=\left\{\begin{matrix}x nếu 0\leq x\frac{1}{2}\\ 1 nếu \frac{1}{2}<x\leq 1 \end{matrix}\right.$ với đồ thị tương ứng như Hình 5.7

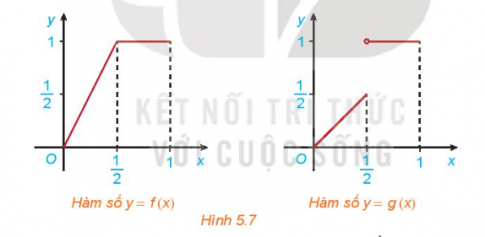
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm $x=\frac{1}{2}$ và nhận xét sụ khác nhau giữa hai đồ thị

Luyện tập 2 trang 121 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tìm các khoảng trên đó hàm số $f(x)=\frac{x^{2}+1}{x+2}$

3. Một số tính chất cơ bản

Hoạt động 3 trang 121 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hai hàm số $f(x)=x^{2}$ và g(x) = -x + 1

a) Xét tính liên tục của hai hàm số trên tại x = 1

b) Tính $L=\underset{x\rightarrow 1}{lim}[f(x)+g(x)]$ và so sánh L với f(1) + g(1)

Vận dụng trang 122 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Giải bài toán ở tình huống mở đầu

Bài tập

Bài tập 5.14 trang 122 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho f(x) và g(x) là các hàm số liên tục tại x = 1. Biết f(1) = 2 và $\underset{x\rightarrow 1}{lim}[2f(x)-g(x)]=3$. Tính g(1)

Bài tập 5.15 trang 122 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Xét tính liên tục của các hàm số sau trên tập xác định của chúng

a) $f(x)=\frac{x}{x^{2}+5x+6}$

b) $f(x)=\left\{\begin{matrix}1+x^{2} nếu x<1\\ 4-x nếu x\geq 1 \end{matrix}\right.$

Bài tập 5.16 trang 122 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Tìm giá trị của tham số m để hàm số $f(x)=\left\{\begin{matrix}sinx nếu x\geq 0\\ -x+m nếu x<0\end{matrix}\right.$ liên tục trên R

Bài tập 5.17 trang 122 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Một bảng giá cước taxi được cho như sau:

a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường đi chuyển

b) Xét tính liên tục của hàm số ở câu a