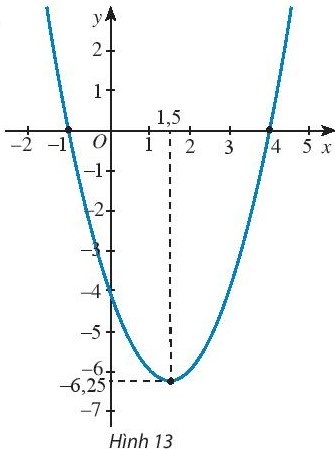
Bài tập 8. Tìm công thức của hàm số đồ thị bậc hai có đồ thị như Hình 13.
Câu hỏi:
Bài tập 8. Tìm công thức của hàm số đồ thị bậc hai có đồ thị như Hình 13.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Đạt
Câu trả lời chi tiết hơn:Để tìm công thức của hàm số đồ thị bậc hai có đồ thị như Hình 13, ta cần xác định được hệ số của hàm số đó. Gọi hàm số cần tìm có dạng y = ax^2 + bx + c.Với việc đồ thị hàm số đi qua các điểm (-1, 0), (4, 0) và (1.5, 6.25), ta có thể lập hệ phương trình sau:1a - 1b + c = 0 (đi qua điểm (-1, 0))16a + 4b + c = 0 (đi qua điểm (4, 0))2.25a + 1.5b + c = -6.25 (đi qua điểm (1.5, 6.25)Giải hệ phương trình trên, ta sẽ có được a = 1, b = -3, c = -4.Vậy hàm số bậc hai cần tìm có công thức là y = x^2 - 3x - 4.
Câu hỏi liên quan:
- Bài tập 1. Hàm số nào sau đây là hàm số bậc hai?a. y = 9$x^{2}$ + 5x + 4 b. y =...
- Bài tập 2. Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai.a. y = m$x^{4}$ + (m + 1)$x^{2}$...
- Bài tập 3. Lập bảng biến thiên của hàm số y =$x^{2}$ + 2x + 3. Hàm số có giá trị lớn nhất hay...
- Bài tập 4. Cho hàm số bậc hai y = f(x) = a$x^{2}$ + bx + c có f(0) = 1; f(1) = 2; f(2) = 5.a. Hãy...
- Bài tập 5. Cho hàm số y = 2$x^{2}$ + x + m. Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ...
- Bài tập 6. Vẽ đồ thị các hàm số sau:a. y = 2$x^{2}$ + 4x - 1b. y = -$x^{2}$ + 2x + 3c. y =...
- Bài tập 7. Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.($P_{1}$) = -2$x^{2}$ -...
- Bài tập 9. Chiếc cầu văng một nhịp được thiết kế hai bên thành cầu dạng parabol và được cố định...






Với bài tập 8 này, cần phân tích đồ thị trong Hình 13 để xác định hệ số a, b, c và từ đó tìm ra công thức của hàm số đồ thị bậc hai.
Sau khi biết các điểm trên đồ thị, ta có thể sử dụng phương pháp giải hệ phương trình hoặc phương pháp suy ra từ hệ số biết sẵn để tìm ra công thức của hàm số đồ thị bậc hai.
Dựa vào hình vẽ đồ thị, chúng ta cần xác định ba điểm trên đồ thị để xác định hệ số của hàm số bậc hai. Các điểm này thường là đỉnh của parabol hoặc điểm cực trị của đồ thị.
Để tìm công thức của hàm số đồ thị bậc hai, ta cần biết ba điểm trên đồ thị hoặc biết hệ số của ba hệ số a, b, c trong phương trình ax^2 + bx + c = 0.