Giải bài tập 2 Hàm số bậc hai
Giải bài tập 2 Hàm số bậc hai: "Sách chân trời sáng tạo toán lớp 10 tập 1"
Trong cuốn sách "Hàm số bậc hai - sách chân trời sáng tạo toán lớp 10 tập 1", việc giải các bài tập trở nên dễ dàng hơn với phần đáp án chuẩn và hướng dẫn giải chi tiết từng bài tập. Các hàm số trong sách này đều có điểm chung là lũy thừa bậc hai của x, giúp học sinh hiểu rõ về tính chất cơ bản của hàm số bậc hai.
Trong phần Khám phá 1, việc khai triển biểu thức của các hàm số giúp học sinh nắm vững cách sắp xếp theo thứ tự lũy thừa của x giảm dần. Các ví dụ minh họa cụ thể giúp học sinh nhận biết hàm số nào có lũy thừa bậc cao nhất của x là bậc hai.
Trong phần Đồ thị hàm số bậc hai, việc xem xét đồ thị của các hàm số giúp học sinh hiểu rõ về hình dạng của parabol. Thông qua việc vẽ đồ thị và so sánh hình dạng của đường cong, học sinh có cơ hội thực hành và nắm vững kiến thức.
Sau đó, trong phần Sự biến thiên của hàm số bậc hai, học sinh được hướng dẫn tìm khoảng đồng biến và nghịch biến của hàm số. Việc áp dụng kiến thức vào các bài tập thực hành giúp học sinh rèn luyện kỹ năng phân tích và đưa ra nhận xét.
Cuối cùng, trong phần Ứng dụng của hàm số bậc hai, học sinh được thực hành với bài toán ứng dụng thực tế. Việc tính toán và giải quyết vấn đề giúp học sinh áp dụng kiến thức từ sách vào thực tế và hiểu rõ hơn về ứng dụng của hàm số bậc hai trong cuộc sống.
Tóm lại, cuốn sách "Hàm số bậc hai - sách chân trời sáng tạo toán lớp 10 tập 1" không chỉ cung cấp kiến thức vững chắc mà còn giúp học sinh hiểu rõ về các tính chất và ứng dụng của hàm số bậc hai trong đời sống hàng ngày.
Bài tập và hướng dẫn giải
Bài tập 1. Hàm số nào sau đây là hàm số bậc hai?
a. y = 9$x^{2}$ + 5x + 4
b. y = 3$x^{3}$ + 2x + 1
c. y = -4$(x + 2)^{3}$ + 2(2$x^{3}$ + 1) + 5
d. y = 5$x^{2}$ + $\sqrt{x}$ + 2
Bài tập 2. Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai.
a. y = m$x^{4}$ + (m + 1)$x^{2}$ + x + 3
b. y = (m - 2)$x^{3}$ + (m - 1)$x^{2}$ + 5
Bài tập 3. Lập bảng biến thiên của hàm số y = $x^{2}$ + 2x + 3. Hàm số có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Bài tập 4. Cho hàm số bậc hai y = f(x) = a$x^{2}$ + bx + c có f(0) = 1; f(1) = 2; f(2) = 5.
a. Hãy xác định giá trị của các hệ số a, b, c.
b. Xác định tập giá trị và khoảng biến thiên của hàm số.
Bài tập 5. Cho hàm số y = 2$x^{2}$ + x + m. Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.
Bài tập 6. Vẽ đồ thị các hàm số sau:
a. y = 2$x^{2}$ + 4x - 1
b. y = - $x^{2}$ + 2x + 3
c. y = -3$x^{2}$ + 6x
d. y = 2$x^{2}$ - 5
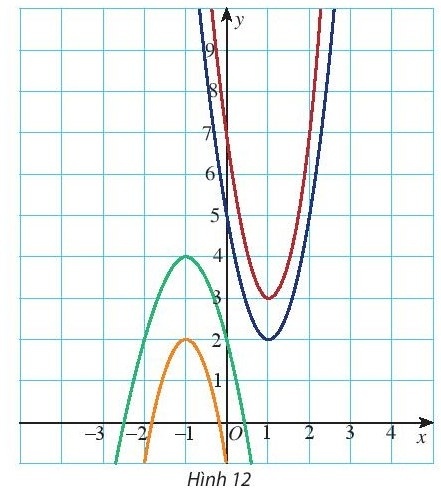
Bài tập 7. Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.
($P_{1}$) = -2$x^{2}$ - 4x + 2;
($P_{2}$) = 3$x^{2}$ - 6x + 5;
($P_{3}$) = 4$x^{2}$ - 8x + 7;
($P_{4}$) = -3$x^{2}$ - 6x - 1.
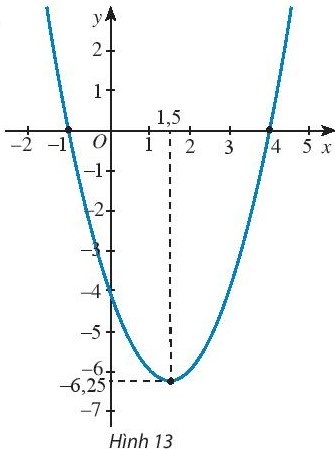
Bài tập 8. Tìm công thức của hàm số đồ thị bậc hai có đồ thị như Hình 13.
Bài tập 9. Chiếc cầu văng một nhịp được thiết kế hai bên thành cầu dạng parabol và được cố định bằng các dây cáp song song.
Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai bên. Biết:
- Dây dài nhất là 5m, dây ngắn nhất là 0,8m. Khoảng cách giữa các dây bằng nhau.
- Nhịp cầu dài 30m.
- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.
