Giải bài tập 3 Giải tam giác và ứng dụng thực tế
Giải bài tập 3: Giải tam giác và ứng dụng thực tế
Sách "Giải bài tập 3: Giải tam giác và ứng dụng thực tế" là một tài liệu hữu ích cho các học sinh lớp 10 trong việc rèn luyện kỹ năng giải các bài toán liên quan đến tam giác. Sách cung cấp phần đáp án chuẩn và hướng dẫn giải chi tiết cho từng bài tập, giúp học sinh hiểu rõ và nắm vững kiến thức bài học.
Trong phần khởi động của sách, việc áp dụng định lí côsin để tính khoảng cách giữa hai điểm trên bờ sông là một ví dụ minh họa cho việc kết hợp kiến thức toán học và thực tế. Việc giải các bài tập về tam giác cũng được hướng dẫn chi tiết, từ việc tính các góc và cạnh của tam giác đến áp dụng các định lí sin, côsin để giải quyết bài toán.
Ngoài ra, sách cũng áp dụng kiến thức toán học vào thực tế thông qua các bài tập vận dụng. Ví dụ như việc tính khoảng cách giữa hai máy bay di chuyển theo hướng khác nhau, hay xác định khoảng cách giữa các thành phố trên bản đồ. Các bài toán này giúp học sinh nhận ra tầm quan trọng của toán học trong cuộc sống hằng ngày.
Với cách trình bày sinh động, sắc nét và dễ hiểu, sách "Giải bài tập 3: Giải tam giác và ứng dụng thực tế" không chỉ giúp học sinh rèn luyện kỹ năng toán học mà còn giúp họ nhận thức được ứng dụng thực tiễn của kiến thức mình học.
Bài tập và hướng dẫn giải
Bài tập 1. Giải tam giác ABC trong các trường hợp sau:
a. AB = 14; AC = 23, $\widehat{A}$ = $125^{\circ}$;
b. BC = 22, $\widehat{B}$ = $64^{\circ}$; $\widehat{C}$ = $38^{\circ}$;
c. AC = 22, $\widehat{B}$ = $120^{\circ}$, $\widehat{C}$ = $28^{\circ}$;
d. AB = 23; AC = 32; BC = 44.
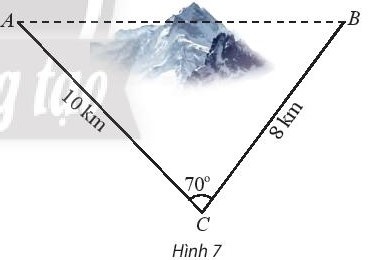
Bài tập 2. Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8km. Góc tạo bởi hai đoạn dây AC và CB là $70^{\circ}$. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
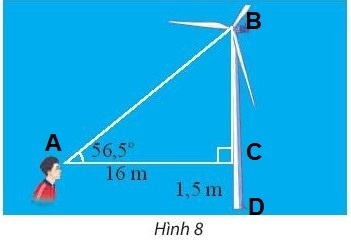
Bài tập 3. Một người đứng cách thân một cái quạt gió 16m và nhìn thầy tâm của cánh quạt với góc nâng $56,5^{\circ}$ (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đât là 1,5m.
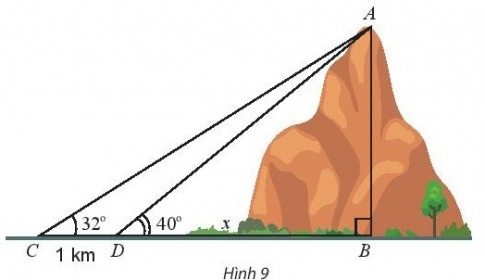
Bài tập 4. Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là $32^{\circ}$ và $40^{\circ}$ (Hình 9).
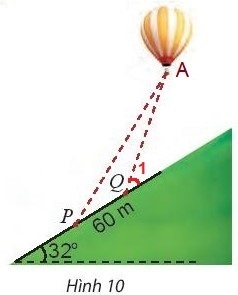
Bài tập 5. Hai người quan sát khinh khí cầu tại hai điểm P và Q nằm ở sườn đồi nghiêng $32^{\circ}$ so với phương ngang, cách nhau 60m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là $62^{\circ}$. Cùng lúc đó, người quan sát tại Q xác định góc nâng của khinh khí cầu là $70^{\circ}$. Tính khoảng cách từ Q đến khinh khí cầu.
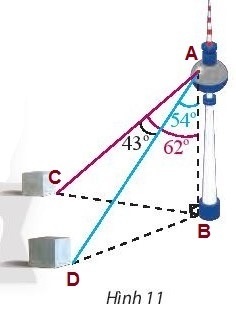
Bài tập 6. Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là $43^{\circ}$, góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là $62^{\circ}$ và điểm mốc khác là $54^{\circ}$ (Hình 11). Tính khoảng cách giữa hai cột mốc này.
