Câu 5: Trang 12 sách phát triển năng lực toán lớp 9 tập 1Dựng các đoạn thẳng có độ...
Câu hỏi:
Câu 5: Trang 12 sách phát triển năng lực toán lớp 9 tập 1
Dựng các đoạn thẳng có độ dài $\sqrt{2}$; $\sqrt{3}$; $\sqrt{5}$; .... (đơn vị: cm).
Bước 1: Dựng tam giác vuông cân ABC có độ dài cạnh góc vuông là 1cm.
Bước 2: Dựng tam giác BCC1 vuông tại C có độ dài CC1 = 1 cm (như hình bên).
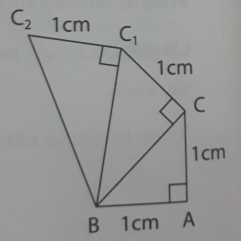
Bước 3: Tiếp tục dựng tam giác BC1C2 vuông tại C1 có độ dài C1C2 = 1cm.
a. Tính độ dài các cạnh BC, BC1, BC2.
b. Tiếp tục dựng các tam giác vuông BC2C3, BC3C4, BC4C5,... theo cách tương tự ở trên. Em có nhận xét gì và độ dài cạnh huyền của tam giác vuông đó.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Vương
Phương pháp giải:a. - Ta có tam giác vuông cân ABC với cạnh góc vuông độ dài 1cm.- Dựng tam giác BCC1 vuông tại C với cạnh CC1 có độ dài 1cm.- Dựng tam giác BC1C2 vuông tại C1 với cạnh C1C2 có độ dài 1cm.Ta tính độ dài các cạnh:- BC = $\sqrt{1^{2}+1^{2}}$ = $\sqrt{2}$- BC1 = $\sqrt{1^{2}+(\sqrt{2})^{2}}$ = $\sqrt{3}$- BC2 = $\sqrt{1^{2}+(\sqrt{3})^{2}}$ = $\sqrt{4}$ = 2b.Tiếp tục dựng các tam giác vuông BC2C3, BC3C4, BC4C5,... theo cách tương tự, ta có độ dài của cạnh huyền của các tam giác vuông lần lượt là:- Tam giác BC2C3: $\sqrt{5}$- Tam giác BC3C4: $\sqrt{6}$- Tam giác BC4C5: $\sqrt{7}$- Và tiếp tục lặp lại quy trình, ta sẽ được các đoạn thẳng có độ dài $\sqrt{5}$, $\sqrt{6}$, $\sqrt{7}$,...
Câu hỏi liên quan:
- Câu 1: Trang 11 sách phát triển năng lực toán lớp 9 tập 1Tìm căn bậc hai số học của các số sau:a....
- Câu 2: Trang 11 sách phát triển năng lực toán lớp 9 tập 1Tìm căn bậc hai của các số sau đây bằng...
- Câu 3: Trang 11 sách phát triển năng lực toán lớp 9 tập 1So sánh:a.$\sqrt{131}$...
- Câu 4: Trang 12 sách phát triển năng lực toán lớp 9 tập 1Tìm các số x thỏa mãn:a.$\sqrt{x}$ =...






{ "content1": "a. Ta có: BC = $\sqrt{2}$ cm, BC1 = $\sqrt{3}$ cm, BC2 = $\sqrt{4}$ cm = 2 cm.", "content2": "b. Khi tiếp tục*** các tam giác theo cách trên, ta thấy độ dài các cạnh liên tiếp tăng lên 1 đơn vị so với cạnh trước đó. Do đó, ta có thể suy luận rằng độ dài các cạnh sẽ tăng dần theo dãy số tự nhiên. Độ dài cạnh huyền của tam giác vuông sẽ phụ thuộc vào số lần tiếp tục*** các tam giác và được tính bằng căn bậc hai của tổng bình phương các độ dài cạnh.", "content3": "Ví dụ: Độ dài cạnh huyền của tam giác thứ n sẽ là $\sqrt{n+1}$."}