Giải bài tập phát triển năng lực toán lớp 9 bài 2: Đường kính và dây cung của đường tròn
Bài tập về đường kính và dây cung của đường tròn
Trong bài tập này, chúng ta sẽ tìm hiểu về đường kính và dây cung của đường tròn. Để bắt đầu, hãy vẽ đường tròn tâm O có đường kính MN = 4cm và vẽ ba dây cung bất kì không phải là đường kính của đường tròn lên hình 2.1. Sau đó, sử dụng thước kẻ để đo độ dài của ba dây cung đó và so sánh với đường kính MN. Khi so sánh, chúng ta sẽ thấy rằng đường kính luôn có độ dài lớn nhất trong một đường tròn. Điều này có thể được chứng minh bằng cách xét hai trường hợp khi một dây cung là đường kính của đường tròn hay không.
Để thực hiện hoạt động này, chúng ta sẽ cần chuẩn bị pa, kéo và giấy. Bước đầu tiên là vẽ một đường tròn lớn trên giấy và cắt rời hình tròn ra. Tiếp theo, gấp phần của hình tròn sao cho không đi qua tâm và mở ra để tạo thành dây cung CD của đường tròn. Sau đó, gấp đôi hình tròn và mở ra, điểm I sẽ là trung điểm của dây cung CD. Sử dụng thước để đo độ và xác định góc tạo bởi đường kính AB và dây cung CD. Chúng ta sẽ nhận thấy rằng đường kính đi qua trung điểm của một dây cung không qua tâm sẽ luôn vuông góc với dây đó.
Từ hoạt động trên, chúng ta cũng có thể rút ra nhận xét rằng trong một đường tròn, đường kính luôn vuông góc với một dây cung khi đi qua trung điểm của dây đó. Bằng cách chứng minh hai trường hợp với dây cung đi qua tâm và không đi qua tâm, bạn sẽ hiểu rõ hơn nguyên lý này. Điều này giúp chúng ta hiểu rõ hơn về mối quan hệ giữa đường kính và dây cung của một đường tròn.
Bài tập và hướng dẫn giải
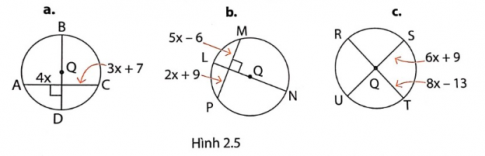
1. Cho đường tròn (Q). Tìm x trong những trường hợp dưới đây (Hình 2.5):
2. Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm bất kì thuộc cung BC không chứa A. Gọi D, E theo thứ tự là các điểm đối xưng với M qua AB, AC (hình 2.6).
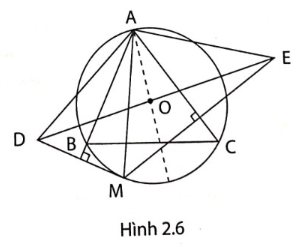
a, Chứng minh rằng tam giác ADM và tam giác AME là các tam giác cân.
b, Chứng minh rằng $\widehat{DAE}=2\widehat{BAC}$
c, Gọi H là hình chiếu của A trên DE. Đặt $\widehat{HAE}=\alpha $. Viết biểu thức thể hiện mối liên hệ giữa $\alpha $, AE và DE.
d, Tìm vị trí của M trên cung BC để DE có độ dài lớn nhất.
3. Hai bạn Hà và Châu viết kết luận về các dây cung của đường tròn (F) vào các tờ giấy dưới đây. Em hãy cho biết bạn nào viết đúng. Giải thích.
| Hình vẽ | Hà | Châu |
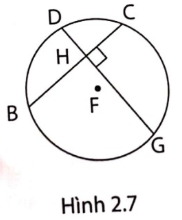 | Vì DG $\perp $ BC nên DG là đường trung trực của BC | Tuy DG $\perp $ BC, nhưng DG không là đường trung trực của BC vì DG không là đường kính. |
4. Trong một bản tin thời sự có phát thông tin về một vụ tai nạn giao thông trên núi. Theo lời nhân chứng kể lại chiếc xe ô tô đã di chuyển với tốc độ rất lớn. Khi gặp khúc cua, chiếc xe đã phanh gấp và bị đâm vào vách núi. Dấu vết của bánh xe hằn lên trên đường thành một hình vòng cung như hình 2.8. Em hãy thực hiện các yêu cầu dưới đây để tìm vận tốc tối đa của chiếc xe lúc đó nhé.
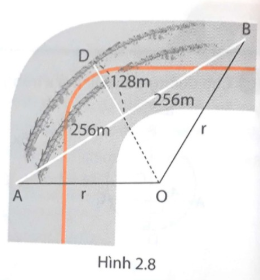
a, Tính bán kính r của cung tròn.
b, Biết rằng $S=3,16\sqrt{f.r}$ là công thức tính vận tốc tối đa của chiếc xe (m/s), trong đó r là bán kính của cung tròn (m) và f là hệ số ma sát của mặt đường. Giả sử f = 0,7, hãy tính vận tốc tối đa của chiếc xe khi xảy ra tai nạn theo đơn vị km/h.
5. Cho nửa đường tròn tâm O đường kính AB, dây CD khác AB. Gọi I là hình chiếu của O trên dây CD.
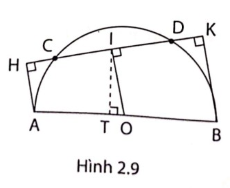
a, Chứng minh rằng I là trung điểm của CD
b, Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ A, B đến CD. Chứng minh rằng I là trung điểm của HK.
c, Gọi T là hình chiếu của I trên AB. Chứng minh rằng SACB + SADB = IT.AB
d, Tìm vị trí của dây CD để diện tích tứ giác AHKB là lớn nhất.





