Bài 6 :Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên...
Câu hỏi:
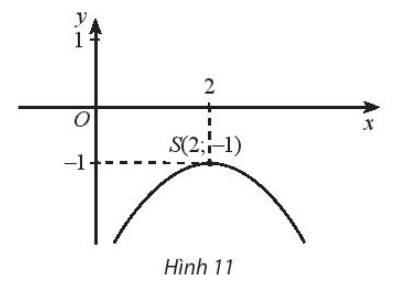
Bài 6 : Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên của hàm số biết đồ thị hàm số là một parabol có đỉnh S như Hình 11.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ngọc
Phương pháp giải:1. Xác định hàm số là hàm số bậc hai do đồ thị là một parabol.2. Tìm đỉnh của parabol (hàm số) bằng cách đổi hàm số về dạng chuẩn.3. Xác định tập xác định D của hàm số.4. Vẽ bảng biến thiên của hàm số để tìm giá trị lớn nhất, tập giá trị và các khoảng biến thiên.Câu trả lời chi tiết:- Hàm số là hàm số bậc hai với đỉnh S(2, -1).- Tập xác định D = ℝ.- Bảng biến thiên của hàm số như sau: + Đồng biến trên (-∞; 2) + Nghịch biến trên (2; +∞)- Giá trị lớn nhất của hàm số là -1 nên tập giá trị T = (– ∞; – 1].Do đó, tập xác định của hàm số là ℝ, giá trị lớn nhất của hàm số là -1, tập giá trị là (– ∞; – 1] và hàm số đồng biến trên khoảng (-∞; 2) và nghịch biến trên khoảng (2; + ∞).
Câu hỏi liên quan:
- Bài 1 :Hàm số nào trong các hàm sau đây không phải là hàm số bậc hai?a) y = 3$x^{2}$ + x...
- Bài 2 :Cho hàm số bậc hai có đồ thị là parabol có đỉnh S, đi qua các điểm A, B, C(0; – 1)...
- Bài 3 :Tìm công thức của hàm số có đồ thị vẽ được ở Bài tập 2.
- Bài 4 :Tìm công thức hàm số bậc hai biết:a) Đồ thị hàm số đi qua 3 điểm A(1; – 3), B(0; – 2),...
- Bài 5 :Tìm khoảng biến thiên và tập giá trị của các hàm số sau:a) y = f(x) = – 2x2– 4x...
- Bài 7 :Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu Nhật Tân lày = f(x) =...
Bình luận (0)





