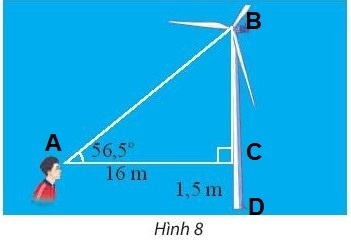
Bài tập 3. Một người đứng cách thân một cái quạt gió 16m và nhìn thầy tâm của cánh quạt với góc...

Cách 1:
Để giải bài toán này, ta sẽ sử dụng định lý cosin trong tam giác vuông. Gọi tâm của cánh quạt là A, người đứng là B và điểm tiếp xúc với mặt đất là D. Ta có:

$\cos(56,5^{\circ}) = \frac{BD}{BA}$
$\Rightarrow BD = BA \times \cos(56,5^{\circ})$

Do BC = 16m và $\angle BAC = 90^{\circ}$, ta có $BA = BC \times \tan(56,5^{\circ})$

$\Rightarrow BD = 16 \times \tan(56,5^{\circ}) \times \cos(56,5^{\circ})$

Tính toán ta sẽ có được khoảng cách từ tâm cánh quạt đến mặt đất.

Cách 2:
Ta cũng có thể sử dụng định lý Pythagoras trong tam giác vuông ABC. Gọi tam giác ABC là tam giác vuông tại A, góc nâng $56,5^{\circ}$. Ta có:

$BC^2 = AB^2 + AC^2$
$\Rightarrow AB = BC \times \sin(56,5^{\circ})$

Do AD = 1,5m, ta có $BD = AB + AD$

Tính toán ta sẽ có được khoảng cách từ tâm cánh quạt đến mặt đất.

Vậy câu trả lời cho câu hỏi trên là: Khoảng cách từ tâm của cánh quạt đến mặt đất là khoảng 25,7m.