Bài tập 4. Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất...
Câu hỏi:
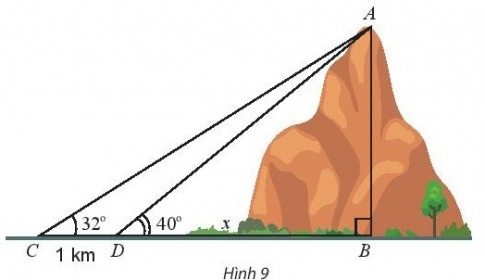
Bài tập 4. Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là $32^{\circ}$ và $40^{\circ}$ (Hình 9).
Câu trả lời:
Người trả lời: GV. Đỗ Văn Việt
Để tính chiều cao AB của một ngọn núi, chúng ta có thể thực hiện các bước sau:1. Vẽ hình với các thông tin đã cho, gồm 2 đoạn thẳng CD và AD, các góc nâng và cạnh AB cần tính.2. Sử dụng định lí sin trong tam giác CAD: $\frac{CD}{sin\widehat{ACD}} = \frac{AD}{sinC}$3. Tính được độ dài AD từ phương trình trên.4. Xét tam giác ADB vuông tại B, áp dụng công thức sin trong tam giác vuông: AB = AD.sinD5. Tính được độ dài AB (chiều cao của ngọn núi).Vậy câu trả lời cho câu hỏi trên là: Ngọn núi có chiều cao khoảng 2,4 km.
Câu hỏi liên quan:
- Bài tập 1. Giải tam giác ABC trong các trường hợp sau:a. AB = 14; AC = 23, $\widehat{A}$ =...
- Bài tập 2. Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên...
- Bài tập 3. Một người đứng cách thân một cái quạt gió 16m và nhìn thầy tâm của cánh quạt với góc...
- Bài tập 5. Hai người quan sát khinh khí cầu tại hai điểm P và Q nằm ở sườn đồi nghiêng $32^{\circ}$...
- Bài tập 6. Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định...
Vì vậy, để tính chiều cao AB của ngọn núi theo các thông tin đã được cung cấp, ta cần thực hiện các bước tính toán và giải phương trình tương ứng.
Kết hợp các thông tin này, ta có thể tạo các phương trình và giải hệ phương trình để tìm ra chiều cao AB của ngọn núi.
Tiếp theo, ta sử dụng thông tin về hai điểm C và D cách nhau 1 km để xác định các tỉ số phía trên của tam giác ABC và tam giác ABD.
Từ thông tin về góc nâng tại C và D, ta có thể xác định được tỉ số CD/AC và CD/BD.
Gọi h là chiều cao của ngọn núi, ta có thể xác định góc ACD và góc ABD thông qua thông tin về góc nâng tại hai điểm C và D.