B. Tự luậnBài tập 1. Trên bàn có một tấm bìa hình tròn được chia thành 10 hình quạt bằng nhau và...
Câu hỏi:
B. Tự luận
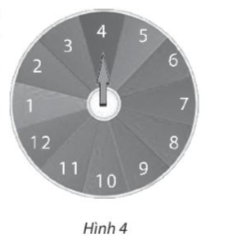
Bài tập 1. Trên bàn có một tấm bìa hình tròn được chia thành 10 hình quạt bằng nhau và được đánh số từ 1 đến 10 như Hình 1. Cường quay mũi tên ở tâm 3 lần và quan sát xem khi mỗi lần dừng lại nó chỉ vào ô số mấy. Tính xác suất của các biến cố sau:
A: “Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ”;
B: “Tích 3 số mũi tên chỉ vào là số chia hết cho 5”.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Ánh
Để giải bài toán này, ta cần phân tích từng bước quay của mũi tên và xác định xác suất của mỗi biến cố.Phương pháp giải:1. Xác định xác suất để mũi tên chỉ vào ô số lẻ: Vì có 5 ô số lẻ và 10 ô trên bảng, nên xác suất để mũi tên chỉ vào ô số lẻ sau mỗi lần quay là $\frac{5}{10} = \frac{1}{2}$. Vậy xác suất để mũi tên chỉ vào ô số lẻ trong 3 lần quay là $(\frac{1}{2})^{3} = \frac{1}{8}$.2. Xác định xác suất để tích của 3 số mũi tên chỉ vào là số chia hết cho 5: Số chia hết cho 5 có thể là 0 hoặc 5. Để tích của 3 số chia hết cho 5, ta phải có ít nhất một số 0 hoặc ba số chia hết cho 5. Xác suất để mũi tên chỉ vào ô số 0 hoặc chia hết cho 5 là $\frac{2}{10} = \frac{1}{5}$. Vậy xác suất để tích của 3 số mũi tên chỉ vào là số chia hết cho 5 là $1 - \frac{8^{2}}{10^{3}} = \frac{61}{125}$.Vậy câu trả lời đúng và chi tiết hơn là:A: "Cả 3 lần mũi tên đều chỉ vào ô ghi số lẻ": $P(A) = \frac{1}{8}$B: "Tích 3 số mũi tên chỉ vào là số chia hết cho 5": $P(B) = \frac{61}{125}$
Câu hỏi liên quan:
- A. Trắc nghiệmBài tập 1. Một hộp có 4 viên bi xanh, 5 viên bi đỏ có kích thước và khối lượng như...
- Bài tập 2. Gieo 2 con xúc xắc cân đối và đồng chất. Xác suất để tích số chấm xuất hiện bằng 7 là:A....
- Bài tập 3. Tung 3 đồng xu cân đối và đồng chất. Xác suất để có ít nhất một đồng xu xuất hiện mặt...
- Bài tập 4. Một hộp chứa 2 loại bi xanh và đỏ. Lấy ra ngẫu nhiên từ hộp 1 viên bi. Biết xác suất lấy...
- Bài tập 5. Gieo một con xúc xắc bốn mặt cân đối và đồng chất ba lần. Xác suất xảy ra biến cố “Có ít...
- Bài tập 6. Chọn ra ngẫu nhiên 2 người từ 35 người trong lớp của Hùng. Xác suất xảy ra biến cố “Hùng...
- Bài tập 7. Xếp 4 quyển sách toán và 2 quyển sách văn thành một hàng ngang trên giá sách một cách...
- Bài tập 8. Cô giáo chia tổ của Lan và Phương thành hai nhóm, mỗi nhóm gồm 4 người để làm việc nhóm...
- Bài tập 2. Mật khẩu mở máy tính của An gồm 8 kí tự, trong đó 2 kí tự đầu là chữ số, 6 kí tự sau là...
- Bài tập 3.Tổ 3 có 6 bạn là Hoà, Hiên, Hiệp, Hương, Thành và Khánh. Chọn ngẫu nhiên 2 bạn...
- Bài tập 4. Một hộp có 5 lá thăm cùng loại được đánh số 2; 4; 6; 8; 10. Lấy ra ngẫu nhiên từ hộp 2...
- Bài tập 5. Doanh nghiệp A chọn ngẫu nhiên 2 tháng trong năm 2020 để tri ân khách hàng. Doanh nghiệp...
- Bài tập 6. Lớp học của hai bạn Hà và Giang có 32 học sinh. Cô giáo chia các bạn vào 4 tổ, mỗi tổ có...
- Bài tập 7. Một hộp chứa 2 quả bóng xanh và một số quả bóng trắng. Lấy ra ngẫu nhiên 2 quả bóng từ...
Bình luận (0)





