CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 1 Góc lượng giác
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 2 Giá trị lượng giác của một góc lượng giác
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 3 Các công thức lượng giác
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 4 Hàm số lượng giác và đồ thị
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 5 Phương trình lượng giác cơ bản
- Giải bài tập toán lớp 11 chân trời sáng tạo Bài tập cuối chương I
CHƯƠNG II. DÃY SỐ. CẤP SỐ CỘNG, CẤP SỐ NHÂN
CHƯƠNG III. GIỚI HẠN. HÀM SỐ LIÊN TỤC
CHƯƠNG IV. ĐƯỜNG THẲNG VÀ MẶT PHẲNG. QUAN HỆ SONG SONG TRONG KHÔNG GIAN
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 1 Điểm, đường thẳng và mặt phẳng trong không gian
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 2 Hai đường thẳng song song
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 3 Đường thẳng và mặt phẳng song song
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 4 Hai mặt phẳng song song
- Giải bài tập toán lớp 11 chân trời sáng tạo bài 5 Phép chiếu song song
- Giải bài tập toán lớp 11 chân trời sáng tạo Bài tập cuối chương IV
CHƯƠNG V. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CHO MẪU SỐ LIỆU GHÉP NHÓM
Giải bài tập toán lớp 11 chân trời sáng tạo bài 2 Giá trị lượng giác của một góc lượng giác
https://s.shopee.vn/AKN2JyAJAw
Giải bài 2: Giá trị lượng giác của một góc lượng giác sách toán lớp 11 tập 1 chân trời sáng tạo. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài
Bài tập và hướng dẫn giải
Câu hỏi mở đầu
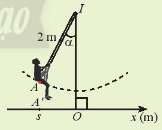
Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A' là hình chiếu của A lên Ox. Toạ độ s của A' trên trục Ox được gọi là li độ A và (IO,IA) = $\alpha $ được gọi là li độ góc của A. Làm các nào để tính li độ dựa vào li độ góc?
1. Giá trị lượng giác của góc lượng giác
Khám phá 1 trang 13 toán lớp 11 Chân trời: Trong Hình 1, M và N lần lượt là các điểm biểu diễn của các góc lượng giác $\frac{2\pi }{3}$ và $\frac{-\pi }{4}$ trên đường tròn lượng giác. Xác định toạ độ của M và N trong hệ trục toạ độ Oxy.

Thực hành 1 trang 15 toán lớp 11 Chân trời: Tính $sin\left ( -\frac{2\pi }{3} \right )$ và $tan\left ( 495^{o} \right )$
2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay
Thực hành 2 trang 16 toán lớp 11 Chân trời: Sử dụng máy tính cầm tay để tính $cos75^{o}$ và $tan\left ( \frac{-19\pi }{6} \right )$.
3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
Khám phá 2 trang 16 toán lớp 11 Chân trời:
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác $\alpha $ trên đường tròn lượng giác. Giải thích vì sao $sin^{2}\alpha + cos^{2}\alpha = 1 $.
b) Khi $cos\alpha \neq 0$, chia cả hai vế của biểu thức câu a) cho $cos^{2}\alpha$ ta được đẳng thức nào?
c) Khi $sin\alpha \neq 0$, chia cả hai vế của biểu thức câu a) cho $sin^{2}\alpha$ ta được đẳng thức nào?

Thực hành 3 trang 17 toán lớp 11 Chân trời: Cho $tan\alpha =\frac{2}{3}$ với $\pi <\alpha <\frac{3\pi }{2}$. Tính $cos\alpha $ và $sin\alpha $
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
Thực hành 4 trang 19 toán lớp 11 Chân trời:
a) Biểu diễn $cos638^{o}$ qua giá trị lượng giác của góc có số đo từ $0^{o}$ đến $45^{o}$
b) Biểu diễn $cot\frac{19\pi }{5}$ qua giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$
Vận dụng trang 19 toán lớp 11 Chân trời: Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu với điểm B và C.
a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng (13 + 10sin$\alpha $) mét với $\alpha $ là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so vói mặt đất khi $\alpha = -30^{o}$
b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm

Bài tập
Bài tập 1 trang 19 toán lớp 11 tập 1 Chân trời: Các đẳng thức sau có thể đồng thời xảy ra không?
a) $sin\alpha = \frac{3}{5}$ và $cos\alpha = -\frac{4}{5}$
b) $sin\alpha = \frac{1}{3}$ và $cot\alpha = \frac{1}{2}$
c) $tan\alpha = 3$ và $cot\alpha = \frac{1}{3}$
Bài tập 2 trang 19 toán lớp 11 tập 1 Chân trời: Cho $sin\alpha = \frac{12}{13}$ và $cos\alpha = \frac{-5}{13}$. Tính $sin\left (- \frac{15\pi }{2} -\alpha \right ) - cos\left ( 13\pi +\alpha \right )$
Bài tập 3 trang 19 toán lớp 11 tập 1 Chân trời: Tính các giá trị lượng giác của góc $\alpha $, nếu:
a) $sin\alpha = \frac{5}{13}$ và $\frac{\pi }{2} < \alpha < \pi $
b) $cos\alpha = \frac{2}{5}$ và $0^{o}<\alpha <90^{o}$
c) $tan\alpha = \sqrt{3}$ và $\pi < \alpha < \frac{3\pi }{2} $
d) $cot\alpha = \frac{1}{2}$ và $270^{o}<\alpha <360^{o}$
Bài tập 4 trang 19 toán lớp 11 tập 1 Chân trời: Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$ hoặc từ $0^{o}$ đến $45^{o}$ và tính:
a) $cos\frac{21\pi }{6}$
b) $sin\frac{129\pi }{4}$
c) $tan1020^{o}$
Bài tập 5 trang 19 toán lớp 11 tập 1 Chân trời: Chứng minh các đẳng thức lượng giác sau:
a) $sin^{4}\alpha - cos^{4}\alpha = 1 - 2cos^{2}\alpha $
b) $tan\alpha + cot\alpha = \frac{1}{sin\alpha .cos\alpha }$
Bài tập 6 trang 19 toán lớp 11 tập 1 Chân trời: Rút gọn các biểu thức sau:
a) $\frac{1}{tan\alpha +1}+\frac{1}{cot\alpha + 1}$
b) $cos(\frac{\pi }{2}-\alpha )-sin(\pi +\alpha )$
c) $sin(\alpha -\frac{\pi }{2}) + cos(-\alpha +6\pi ) - tan(\alpha +\pi )cot(3\pi -\alpha )$
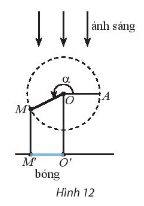
Bài tập 7 trang 20 toán lớp 11 tập 1 Chân trời: Thanh OM quay ngược chiều kim đồng hồ quanh gốc O của nó trên một mặt phẳng đứng và in bóng vuông góc xuông mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O'M' của OM khi thanh quay được $3\frac{1}{10}$ vòng là bao nhiêu. Biết độ dài thanh OM là 15cm? Kết quả làm tròn đến hàng phần mười.
Bài tập 8 trang 20 toán lớp 11 tập 1 Chân trời: Khi xe đạp di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau 1 phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58cm? Giả sử độ dày của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.

Giải bài tập sách giáo khoa (SGK) lớp 11 kết nối tri thức
- Soạn ngữ văn lớp 11 kết nối tri thức
- Văn mẫu lớp 11 kết nối tri thức
- Soạn ngữ văn lớp 11 tập 1 kết nối tri thức
- Soạn ngữ văn lớp 11 tập 2 kết nối tri thức
- Giải bài tập toán lớp 11 tập 1 kết nối tri thức
- Giải bài tập toán lớp 11 tập 2 kết nối tri thức
- Giải bài tập vật lí lớp 11 kết nối tri thức
- Giải bài tập hóa học lớp 11 kết nối tri thức
- Giải bài tập sinh học lớp 11 kết nối tri thức
- Giải bài tập lịch sử lớp 11 kết nối tri thức
- Giải bài tập địa lí lớp 11 kết nối tri thức
- Giải bài tập kinh tế pháp luật lớp 11 kết nối tri thức
- Giải bài tập âm nhạc lớp 11 kết nối tri thức
- Giải bài tập mĩ thuật lớp 11 kết nối tri thức
- Giải bài tập quốc phòng an ninh lớp 11 kết nối tri thức
- Giải bài tập công nghệ chăn nuôi lớp 11 kết nối tri thức
- Giải bài tập công nghệ cơ khí lớp 11 kết nối tri thức
- Giải bài tập tin học lớp 11 định hướng Tin học ứng dụng kết nối tri thức
- Giải bài tập tin học lớp 11 định hướng Khoa học máy tính kết nối tri thức
- Giải bài tập hoạt động trải nghiệm hướng nghiệp lớp 11 kết nối tri thức
Giải bài tập sách giáo khoa (SGK) lớp 11 chân trời sáng tạo
- Soạn ngữ văn lớp 11 chân trời sáng tạo
- Văn mẫu lớp 11 chân trời sáng tạo
- Soạn ngữ văn lớp 11 tập 1 chân trời sáng tạo
- Soạn ngữ văn lớp 11 tập 2 chân trời sáng tạo
- Giải bài tập toán lớp 11 tập 1 chân trời sáng tạo
- Giải bài tập toán lớp 11 tập 2 chân trời sáng tạo
- Giải bài tập vật lí lớp 11 chân trời sáng tạo
- Giải bài tập hóa học lớp 11 chân trời sáng tạo
- Giải bài tập sinh học lớp 11 chân trời sáng tạo
- Giải bài tập lịch sử lớp 11 chân trời sáng tạo
- Giải bài tập địa lí lớp 11 chân trời sáng tạo
- Giải bài tập kinh tế pháp luật lớp 11 chân trời sáng tạo
- Giải bài tập âm nhạc lớp 11 chân trời sáng tạo
- Giải bài tập mĩ thuật lớp 11 chân trời sáng tạo
- Giải bài tập quốc phòng an ninh lớp 11 chân trời sáng tạo
- Giải bài tập hoạt động trải nghiệm hướng nghiệp lớp 11 chân trời sáng tạo bản 1
- Giải bài tập hoạt động trải nghiệm hướng nghiệp lớp 11 chân trời sáng tạo bản 2
Giải bài tập sách giáo khoa (SGK) lớp 11 cánh diều
- Soạn ngữ văn lớp 11 cánh diều
- Văn mẫu lớp 11 cánh diều
- Soạn ngữ văn lớp 11 tập 1 cánh diều
- Soạn ngữ văn lớp 11 tập 2 cánh diều
- Giải bài tập toán lớp 11 tập 1 cánh diều
- Giải bài tập toán lớp 11 tập 2 cánh diều
- Giải bài tập vật lí lớp 11 cánh diều
- Giải bài tập hóa học lớp 11 cánh diều
- Giải bài tập sinh học lớp 11 cánh diều
- Giải bài tập lịch sử lớp 11 cánh diều
- Giải bài tập địa lí lớp 11 cánh diều
- Giải bài tập kinh tế pháp luật lớp 11 cánh diều
- Giải bài tập âm nhạc lớp 11 cánh diều
- Giải bài tập mĩ thuật lớp 11 cánh diều
- Giải bài tập quốc phòng an ninh lớp 11 cánh diều
- Giải bài tập công nghệ chăn nuôi lớp 11 cánh diều
- Giải bài tập công nghệ cơ khí lớp 11 cánh diều
- Giải bài tập tin học lớp 11 định hướng Tin học ứng dụng cánh diều
- Giải bài tập tin học lớp 11 định hướng Khoa học máy tính cánh diều
- Giải bài tập hoạt động trải nghiệm hướng nghiệp lớp 11 cánh diều
Giải bài tập sách bài tập (SBT) lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 11 tập 1 kết nối tri thức
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 11 tập 2 kết nối tri thức
- Giải bài tập sách bài tập (SBT) toán lớp 11 tập 1 kết nối tri thức
- Giải bài tập sách bài tập (SBT) toán lớp 11 tập 2 kết nối tri thức
- Giải bài tập sách bài tập (SBT) sinh học lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) vật lí lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) hóa học lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) địa lí lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) lịch sử lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) kinh tế pháp luật lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) quốc phòng an ninh lớp 11 kết nối tri thức
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm hướng nghiệp lớp 11 kết nối tri thức
Giải bài tập sách bài tập (SBT) lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 11 tập 1 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 11 tập 2 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) toán lớp 11 tập 1 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) toán lớp 11 tập 2 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) sinh học lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) vật lí lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) hóa học lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) lịch sử lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) địa lí lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) kinh tế pháp luật lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) quốc phòng an ninh lớp 11 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm hướng nghiệp lớp 11 chân trời sáng tạo bản 1
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm hướng nghiệp lớp 11 chân trời sáng tạo bản 2
Giải bài tập sách bài tập (SBT) lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 11 tập 1 cánh diều
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 11 tập 2 cánh diều
- Giải bài tập sách bài tập (SBT) toán lớp 11 tập 1 cánh diều
- Giải bài tập sách bài tập (SBT) toán lớp 11 tập 2 cánh diều
- Giải bài tập sách bài tập (SBT) vật lí lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) sinh học lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) hóa học lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) địa lí lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) lịch sử lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) kinh tế pháp luật lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) quốc phòng an ninh lớp 11 cánh diều
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm hướng nghiệp lớp 11 cánh diều
Giải bài tập chuyên đề học tập lớp 11 kết nối tri thức
- Giải bài tập chuyên đề toán lớp 11 kết nối tri thức
- Giải bài tập chuyên đề ngữ văn lớp 11 kết nối tri thức
- Giải bài tập chuyên đề vật lí lớp 11 kết nối tri thức
- Giải bài tập chuyên đề hóa học lớp 11 kết nối tri thức
- Giải bài tập chuyên đề sinh học lớp 11 kết nối tri thức
- Giải bài tập chuyên đề kinh tế pháp luật lớp 11 kết nối tri thức
- Giải bài tập chuyên đề lịch sử lớp 11 kết nối tri thức
- Giải bài tập chuyên đề địa lí lớp 11 kết nối tri thức
- Giải bài tập chuyên đề mĩ thuật lớp 11 kết nối tri thức
- Giải bài tập chuyên đề âm nhạc lớp 11 kết nối tri thức
- Giải bài tập chuyên đề công nghệ chăn nuôi lớp 11 kết nối tri thức
- Giải bài tập chuyên đề công nghệ cơ khí lớp 11 kết nối tri thức
- Giải bài tập chuyên đề tin học lớp 11 định hướng Khoa học máy tính kết nối tri thức
- Giải bài tập chuyên đề tin học lớp 11 định hướng Tin học ứng dụng kết nối tri thức
- Giải bài tập chuyên đề quốc phòng an ninh lớp 11 kết nối tri thức
- Giải bài tập chuyên đề hoạt động trải nghiệm hướng nghiệp lớp 11 kết nối tri thức
Giải bài tập chuyên đề học tập lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề toán lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề ngữ văn lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề vật lí lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề hóa học lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề sinh học lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề lịch sử lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề địa lí lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề âm nhạc lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề mĩ thuật lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề kinh tế pháp luật lớp 11 chân trời sáng tạo
- Giải bài tập chuyên đề hoạt động trải nghiệm hướng nghiệp lớp 11 chân trời sáng tạo bản 1
- Giải bài tập chuyên đề hoạt động trải nghiệm hướng nghiệp lớp 11 chân trời sáng tạo bản 2
- Giải bài tập chuyên đề quốc phòng an ninh lớp 11 chân trời sáng tạo
Giải bài tập chuyên đề học tập lớp 11 cánh diều
- Giải bài tập chuyên đề toán lớp 11 cánh diều
- Giải bài tập chuyên đề ngữ văn lớp 11 cánh diều
- Giải bài tập chuyên đề vật lí lớp 11 cánh diều
- Giải bài tập chuyên đề hóa học lớp 11 cánh diều
- Giải bài tập chuyên đề sinh học lớp 11 cánh diều
- Giải bài tập chuyên đề lịch sử lớp 11 cánh diều
- Giải bài tập chuyên đề địa lí lớp 11 cánh diều
- Giải bài tập chuyên đề kinh tế pháp luật lớp 11 cánh diều
- Giải bài tập chuyên đề mĩ thuật lớp 11 cánh diều
- Giải bài tập chuyên đề âm nhạc lớp 11 cánh diều
- Giải bài tập chuyên đề công nghệ chăn nuôi lớp 11 cánh diều
- Giải bài tập chuyên đề công nghệ cơ khí lớp 11 cánh diều
- Giải bài tập chuyên đề tin học lớp 11 định hướng Tin học ứng dụng cánh diều
- Giải bài tập chuyên đề tin học lớp 11 định hướng Khoa học máy tính cánh diều
- Giải bài tập chuyên đề quốc phòng an ninh lớp 11 cánh diều
- Giải bài tập chuyên đề hoạt động trải nghiệm hướng nghiệp lớp 11 cánh diều




