Bài tập 11. Một xe goòng được kéo bởi một lực$\vec{F}$ có độ lớn là 50N, di chuyển theo quãng...
Câu hỏi:
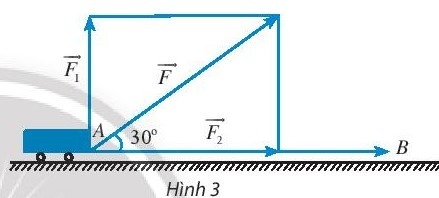
Bài tập 11. Một xe goòng được kéo bởi một lực $\vec{F}$ có độ lớn là 50N, di chuyển theo quãng đường từ A đến B có chiều dài 200m. Cho biết góc giữa $\vec{F}$ và $\vec{AB}$ là $30^{\circ}$ và $\vec{F}$ được phân tích thành hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ (Hình 3). Tính công sinh bởi các lực $\vec{F}$, $\vec{F_{1}}$ và $\vec{F_{2}}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Long
Để tính công sinh bởi các lực $\vec{F}$, $\vec{F_{1}}$ và $\vec{F_{2}}$, ta áp dụng công thức công của lực theo định nghĩa: 1. Lực $\vec{F}$:- $\vec{F_{1}} = \vec{F} \cdot \sin{30^{\circ}} = 50 \cdot \sin{30^{\circ}} = 25$ (N)- $\vec{F_{2}} = \vec{F} \cdot \cos{30^{\circ}} = 50 \cdot \cos{30^{\circ}} = 25\sqrt{3}$ (N)2. Công sinh bởi lực $\vec{F}$:- $A = |\vec{F}| \cdot |\vec{AB}| \cdot \cos{30^{\circ}} = 50 \cdot 200 \cdot \cos{30^{\circ}} = 5000\sqrt{3}$ (J)3. Công sinh bởi lực $\vec{F_{1}}$:- $A_{1} = |\vec{F_{1}}| \cdot |\vec{AB}| \cdot \cos{90^{\circ}} = 0$ (J)4. Công sinh bởi lực $\vec{F_{2}}$:- $A_{2} = |\vec{F_{2}}| \cdot |\vec{AB}| \cdot \cos{0^{\circ}} = 25\sqrt{3} \cdot 200 \cdot 1 = 5000\sqrt{3}$ (J)Vậy câu trả lời chi tiết là:- Công sinh bởi lực $\vec{F}$ là $5000\sqrt{3}$ J- Công sinh bởi lực $\vec{F_{1}}$ là 0 J- Công sinh bởi lực $\vec{F_{2}}$ là $5000\sqrt{3}$ J
Câu hỏi liên quan:
- Bài tập 3.Cho hình thoi ABCD có cạnh bằng a và có góc A bằng $60^{\circ}$. Tìm độ dài các...
- Bài tập 4. Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E...
- Bài tập 5. Cho$\vec{a}$,$\vec{b}$ là hai vectơ khác vectơ$\vec{0}$. Trong trường...
- Bài tập 6. Cho |$\vec{a}$ +$\vec{b}$| = 0. So sánh độ dài, phương và hướng của hai...
- Bài tập 7. Cho bốn điểm A, B, C, D. Chứng minh rằng$\vec{AB}$ =$\vec{CD}$ khi và chỉ...
- Bài tập 8. Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh...
- Bài tập 9. Một chiếc máy bay được biết là đang bay về phía bắc với tốc độ 45 m/s, mặc dù vận tốc...
- Bài tập 10. Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E,...
- Bài tập 12. Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên, dòng...






{ 1. Để tính công sinh bởi lực $\vec{F}$, ta sử dụng công thức $W = \vec{F} \cdot \vec{d} \cdot \cos{\theta}$. 2. Thay vào công thức, ta được công sinh bởi lực $\vec{F}$ là $W = 50 \times 200 \times \cos{30^{\circ}}$ J. 3. Tính toán giá trị trên, ta có công sinh bởi lực $\vec{F}$ là $50 \times 200 \times \cos{30^{\circ}} = 8660.25$ J. 4. Để tính công sinh bởi lực $\vec{F_{1}}$, ta sử dụng công thức $W = \vec{F_{1}} \cdot \vec{d} \cdot \cos{\theta}$. 5. Tiếp tục tương tự, để tính công sinh bởi lực $\vec{F_{2}}$, ta sử dụng công thức $W = \vec{F_{2}} \cdot \vec{d} \cdot \cos{\theta}$.}