Bài tập 5. Xét vị trí tương đối của các cặp đường thẳng $d_{1}$ và $d_{2}$ sau đây:
Câu hỏi:
Bài tập 5. Xét vị trí tương đối của các cặp đường thẳng $d_{1}$ và $d_{2}$ sau đây:
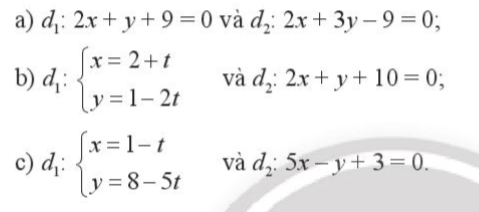
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Giang
Để xác định vị trí tương đối của hai đường thẳng $d_{1}$ và $d_{2}$, ta cần xem xét các trường hợp sau:1. Nếu hai đường thẳng $d_{1}$ và $d_{2}$ cắt nhau tại một điểm duy nhất, tức là không song song và không trùng nhau.2. Nếu hai đường thẳng $d_{1}$ và $d_{2}$ song song với nhau, tức là không cắt nhau và không trùng nhau.3. Nếu hai đường thẳng $d_{1}$ và $d_{2}$ trùng nhau, tức là đường thẳng này là đường thẳng khác biệt nhưng nằm trên cùng một "đường thẳng cơ sở".Vậy, vị trí tương đối của hai đường thẳng $d_{1}$ và $d_{2}$ có thể thuộc vào một trong ba trường hợp trên. Để xác định trường hợp cụ thể, ta cần tham khảo thông tin chi tiết hơn từ bài toán cụ thể hoặc xem xét đồ thị hình học của hai đường thẳng đó.
Câu hỏi liên quan:
- Các bài toán san đây được xét tong mặt phẳng Oxy.Bài tập 1. Tìm các giá trị của tham sô a, b, c để...
- Bài tập 2. Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường...
- Bài tập 3. Cho tam giác ABC, biết A(1; 4), B(0; 1) và C(4; 3).a) Lập phương trình tổng quát của...
- Bài tập 4. Lập phương trình tổng quát của đường thẳng $\Delta$ trong mỗi trường hợp sau:a) $\Delta$...
- Bài tập6. Cho đường thẳng d có phương trình tham số:Tìm giao điểm của d với đường thẳng...
- Bài tập 7. Tìm số đo của góc giữa hai đường thẳng $d_{1}$ và $d_{2}$ trong các trường hợp sau:a)...
- Bài tập 8.Tính khoảng cách từ điềm M đến đường thẳng $\Delta$ trong các trường hợp sau:a)...
- Bài tập 9. Tìm c để đường thẳng $\Delta$: 4x - 3y + c = 0 tiếp xúc với đường tròn (C) có...
- Bài tập10. Tính khoảng cách giữa hai đường thẳng:$\Delta$: 6x + 8y - 11 = 0 và $\Delta'$: 6x...
- Bài tập 11. Một trạm viễn thông S có tọa độ (5, 1). Một người đang ngồi trên chiếc xe khách chạy...
Bình luận (0)





