Giải bài tập sách bài tập (SBT) toán lớp 10 Cánh diều bài Bài tập cuối chương IV
Giải bài tập cuối chương IV sách bài tập toán lớp 10
Bài tập cuối chương IV trang 106 sách bài tập (SBT) toán lớp 10 được hướng dẫn giải chi tiết trong vở học "Cánh diều". Đây là một phần trong bộ sách được biên soạn theo chương trình đổi mới của Bộ Giáo dục. Bài tập này giúp học sinh nắm vững kiến thức và áp dụng chúng vào thực hành. Hướng dẫn giải bài tập cụ thể và chi tiết sẽ giúp học sinh hiểu rõ hơn về bài học.
Bài tập và hướng dẫn giải
Bài 67 : Cho góc nhọn

Bài 68 : Cho các vectơ khác 0. Phát biểu nào sau đây là đúng?

Bài 69 : Cho tứ giác ABCD. Biểu thức

Bài 70 : Cho góc nhọn

Bài 71 :

Bài 72 : Cho tam giác ABC có AB = 4, AC = 6, góc ABC = 60 độ. Tính:

Bài 73 : Cho tam giác ABC, chứng minh
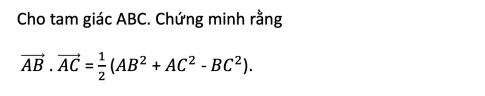
Bài 74 : Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính:

Bài 75 : Cho ba điểm phân biệt I, A, B và số thực khác 1

Bài 76 : Cho tam giác ABC có AB = 4 , AC = 5, góc BAC = 120 độ

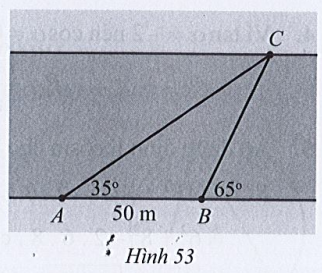
Bài 77 : Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc song chỗ chảy qua vị trí đang đứng (khúc song tương đối thẳng, có thể xem hai bờ song song với nhau).
Từ vị trí đang đứng A, người đó đo được góc nghiêng α = 35° so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đi dọc bờ sông đến vị trí B cách A một khoảng d = 50m và tiếp tục đo được góc nghiêng β = 65° so với bờ sông tới vị trí C đã chọn (Hình 53). Hỏi độ rộng của con sông chỗ chảy qua vị trí người quan sát đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Bài 78 : Cho hai vectơ a và b. Tính
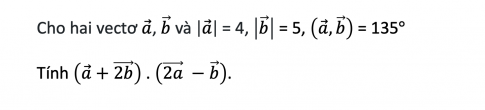
Bài 79 :
a) Chứng minh đẳng thức
b) Cho giá trị vectơ. Tính

Bài 80 : Cho tam giác ABC có ba trung tuyến AD, BE, CF. Chứng minh rằng:

Bài 81* : Cho tứ giác ABCD. M là điểm thay đổi trong mặt phẳng thoả mãn
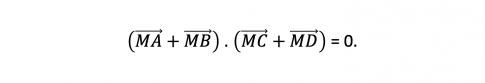
Chứng minh rằng điểm M luôn nằm trên một đường tròn cố định.
Bài 82* : Cho tam giác ABC và đường thẳng d không có điểm chung với bất kì cạnh nào của tam giác. M là điểm thay đổi trên đường thẳng d. Xác định vị trí của M sao cho biểu thức
MA→+MB→+MC→">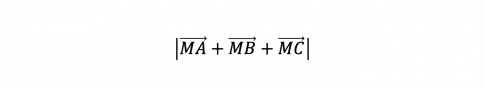
đạt giá trị nhỏ nhất.





