Giải bài tập sách bài tập (SBT) toán lớp 10 Cánh diều bài 4 Bất phương trình bậc hai một ẩn
Hướng dẫn giải bài 4 Bất phương trình bậc hai một ẩn trang 48 vở bài tập (VBT) toán lớp 10
Bài toán bất phương trình bậc hai một ẩn là một trong những bài toán khá phổ biến và quan trọng trong toán học. Để giải bài toán này, chúng ta cần thực hiện các bước sau đây:
- Xác định miền xác định của biến số, tức là tập hợp các giá trị mà biến số có thể nhận.
- Chuyển bài toán về dạng chuẩn bằng cách đưa tất cả các thành phần về cùng một phía của bất phương trình.
- Sử dụng các phép biến đổi để giải bất phương trình bậc hai một ẩn.
- Kiểm tra nghiệm để đảm bảo tính chính xác của kết quả.
Với cách hướng dẫn cụ thể và giải chi tiết, học sinh sẽ dễ dàng nắm bắt và hiểu rõ hơn vấn đề. Đặc biệt, sự cẩn thận và chính xác trong từng bước giải quyết bài toán là rất quan trọng để đạt được kết quả chính xác.
Bài tập và hướng dẫn giải
Bài 28 : Trong các bất phương tình sau, bất phương trình nào không là bất phương trình bậc nhất một ẩn?
A. – 2x2 + 3x < 0.
B. 0,5y2 – 3">√3(y – 2) ≤ 0.
C. x2 – 2xy – 3 ≥ 0.
D. 2">√2x2 – 3 ≥ 0.
Bài 29 : Tập nghiệm của bất phương trình – x2 + 3x + 18 ≥ 0 là:
A. [ – 3; 6].
B. (– 3; 6).
C. (– ∞; – 3) ∪ (6; +∞).
D. (– ∞; – 3] ∪ [6; +∞).
Bài 30 : Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: f(x) > 0; f(x) < 0; f(x) ≥ 0 và f(x) ≤ 0.
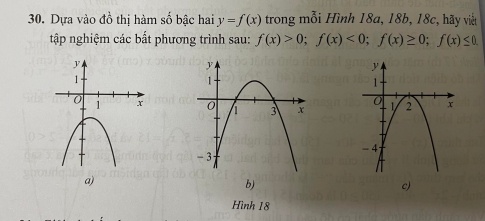
Bài 31 : Giải các bất phương trình bậc hai sau:
a) 3x2 – 8x + 5 > 0.
b) – 2x2 – x + 3 ≤ 0.
c) 25x2 – 10x + 1 < 0.
d) – 4x2 + 5x + 9 ≥ 0.
Bài 32 : Tìm giao các tập nghiệm của hai bất phương trình – 3x2 + 7x + 10 ≥ 0 và – 2x2 – 9x + 11 > 0.
Bài 33 : Tìm m để phương trình – x2 + (m + 2)x + 2m – 10 = 0 có nghiệm.
Bài 34 : Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,3) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8m sau 1 giây và đạt độ cao 6m sau 2 giây. Trong khoảng thời gian nào (tính bằng giây) thì quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m (làm tròn kết quả đến hàng phần nghìn).
Bài 35 : Một tình huống trong huấn luyện pháo binh được mô tả như sau: Trong mặt phẳng tọa độ Oxy (đơn vị trên hai trục tính theo mét), một viên đạn được bắn từ vị trí O(0; 0) theo quỹ đạo là đường parabol y = −91 000 000x2+3100x">−91 000 000x2+3100x">−91 000 000x2+3100x">−91 000 000x2+3100x">−−91 000 000x2+3100x">−91 000 000x2+3100x">9/−91 000 000x2+3100x">−91 000 000x2+3100x">1 −91 000 000x2+3100x">−91 000 000x2+3100x">000 −91 000 000x2+3100x">−91 000 000x2+3100x">000x2 −91 000 000x2+3100x">−91 000 000x2+3100x">−91 000 000x2+3100x">−91 000 000x2+3100x">+ −91 000 000x2+3100x">−91 000 000x2+3100x">3/−91 000 000x2+3100x">100−91 000 000x2+3100x">x−91 000 000x2+3100x">. Tìm khoảng cách theo trục hoành của viên đạn so với vị trí bắn khi viên đạn đang ở độ cao hơn 15 m (làm tròn kết quả đến hàng phần trăm theo đơn vị mét).





