Bài 73 : Cho tam giác ABC, chứng minh
Câu hỏi:
Bài 73 : Cho tam giác ABC, chứng minh
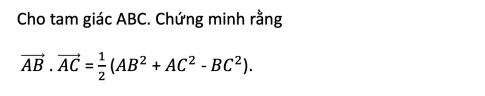
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Long
Phương pháp giải:Để chứng minh rằng tam giác ABC là tam giác vuông, chúng ta cần chứng minh 1 trong 3 điều kiện sau:1. Cạnh huyền của tam giác đó bằng với cạnh nào đó của tam giác đó.2. Có một góc vuông trong tam giác đó.3. Sử dụng định lí Pythagore.Giả sử ta có tam giác ABC với AB = 6, BC = 8, AC = 10.Ta có thể sử dụng định lí Pythagore để chứng minh rằng tam giác ABC là tam giác vuông.Áp dụng định lí Pythagore, ta có: AC^2 = AB^2 + BC^210^2 = 6^2 + 8^2100 = 36 + 64100 = 100Do đó, ta chứng minh được rằng tam giác ABC là tam giác vuông.Câu trả lời cho bài toán: Tam giác ABC là tam giác vuông.
Câu hỏi liên quan:
- Bài 67 : Cho góc nhọn
- Bài 68 :Cho các vectơ khác 0. Phát biểu nào sau đây là đúng?
- Bài 69 : Cho tứ giác ABCD. Biểu thức
- Bài 70 : Cho góc nhọn
- Bài 71 :
- Bài 72 : Cho tam giác ABC có AB = 4, AC = 6, góc ABC = 60 độ. Tính:
- Bài 74 : Cho tam giác ABC có AB = 5, BC = 6, CA = 7. Tính:
- Bài 75 : Cho ba điểm phân biệt I, A, B và số thực khác 1
- Bài 76 : Cho tam giác ABC có AB = 4 , AC = 5, góc BAC = 120 độ
- Bài 77 : Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc song chỗ chảy qua vị trí đang...
- Bài 78 : Cho hai vectơ a và b. Tính
- Bài 79 :a) Chứng minh đẳng thứcb) Cho giá trị vectơ. Tính
- Bài 80 : Cho tam giác ABC có ba trung tuyến AD, BE, CF. Chứng minh rằng:
- Bài 81* : Cho tứ giác ABCD. M là điểm thay đổi trong mặt phẳng thoả mãnChứng minh rằng điểm M...
- Bài 82* :Cho tam giác ABC và đường thẳng d không có điểm chung với bất kì cạnh nào của tam...
Bình luận (0)





