Giải bài tập sách bài tập (SBT) toán lớp 10 Cánh diều bài 2 Giải bài tập tam giác. Tính diện tích
Hướng dẫn giải bài 2 sách Cánh Diều - Tính diện tích tam giác
Bài tập số 2 trang 76 trong sách bài tập toán lớp 10 sách "Cánh diều" yêu cầu chúng ta tính diện tích của một tam giác. Để giải bài này, trước hết chúng ta cần biết công thức tính diện tích của tam giác, đó là S = 0.5 * cơ sở * chiều cao. Sau đó, ta lưu ý rằng cơ sở và chiều cao của tam giác được cho trong đề bài, việc còn lại là thay vào công thức và tính toán ra kết quả.
Bộ sách "Cánh diều" được biên soạn dựa trên chương trình đổi mới của Bộ Giáo dục, với mục tiêu giúp học sinh nắm vững kiến thức toán học một cách chi tiết và cụ thể. Hy vọng rằng với cách hướng dẫn chi tiết và giải thích rõ ràng, học sinh sẽ cảm thấy dễ dàng hơn khi tiếp cận với bài toán này.
Bài tập và hướng dẫn giải
Bài 12 : Cho tam giác ABC có AB = 6,5 cm, AC = 8,5 cm, góc A = 125°. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
Bài 13 : Cho tam giác ABC có BC = 50 cm, góc B^=65°,C^=45°">B^=65°,C^=45°">B^=65°,C^=45°">B^=65°,C^=45°">B^=65°,C^=45°">B^=65°,C^=45°">B = 65°,góc C = 45°. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
Bài 14 : Cho tam giác ABC có AB = 5, AC = 8, BC = 9. Tính (làm tròn kết quả đến hàng phần mười theo đơn vị tương ứng).
a) Số đo các góc A, B, C;
b) Diện tích tam giác ABC.
Bài 15 : Cho tam giác ABC có góc B^=60°">B^=60°">B^=60°">B^=60°">B^=60°">B B^=60°">= B^=60°">60 độ; BC = 8, AB + AC = 12. Tính độ dài các cạnh AB, AC.
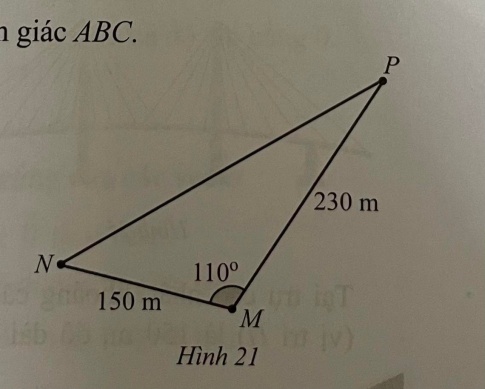
Bài 16 : Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150m, chiều dài của hàng rào MP là 230 m. Góc giữa hai hàng rào MN và MP là 110° (Hình 21).
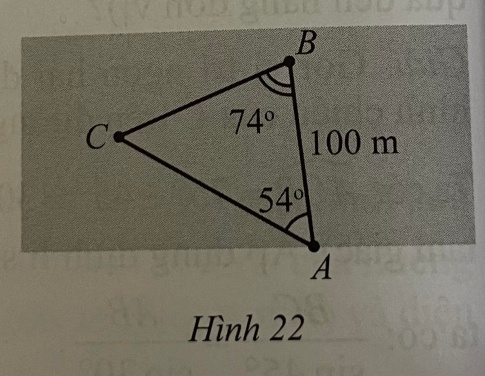
Bài 17 : Hai người A và B cùng quan sát một con tàu đang neo đậu ngoài khơi tại vị trí C. Người A đứng trên bờ biển, người B đứng trên một hòn đảo cách bờ một khoảng AB = 100m. Hai người tiến hành đo đạc và thu được kết quả góc CAB^=54°,CBA^=74°">CAB^=54°,CBA^=74°">CAB^=54°,CBA^=74°">CAB^=54°,CBA^=74°">CAB^=54°,CBA^=74°">CAB^=54°,CBA^=74°">CCAB^=54°,CBA^=74°">ACAB^=54°,CBA^=74°">B CAB^=54°,CBA^=74°">= CAB^=54°,CBA^=74°">54CAB^=54°,CBA^=74°">°CAB^=54°,CBA^=74°">, góc CAB^=54°,CBA^=74°">CAB^=54°,CBA^=74°">CAB^=54°,CBA^=74°">CCAB^=54°,CBA^=74°">BCAB^=54°,CBA^=74°">A CAB^=54°,CBA^=74°">= CAB^=54°,CBA^=74°">74CAB^=54°,CBA^=74°">°CAB^=54°,CBA^=74°">(Hình 22). Hỏi con tàu cách hòn đảo bao xa (làm tròn kết quả đến hàng phần mười theo đơn vị mét)?
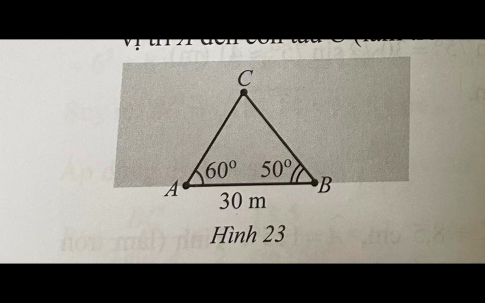
Bài 18 : Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một con tàu C đang neo đậu ngoài khơi. Người đó tiến hành đo đạc và thu được kết quả: AB = 30 m, góc CAB = 60°, góc CBA = 50° (Hình 23). Tính khoảng cách từ vị trí A đến con tàu C (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
Bài 19 : Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m,
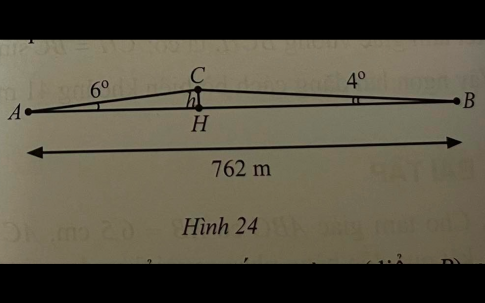
a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng vận tốc trung bình lên dốc là 4km/h và tốc độ khi xuống dốc là 19 km/h.
Bài 20 : Quan sát cây cầu văng minh họa ở Hình 25.
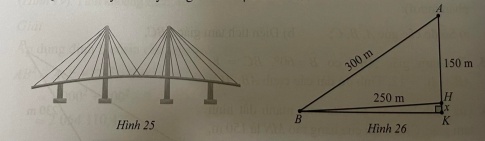
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
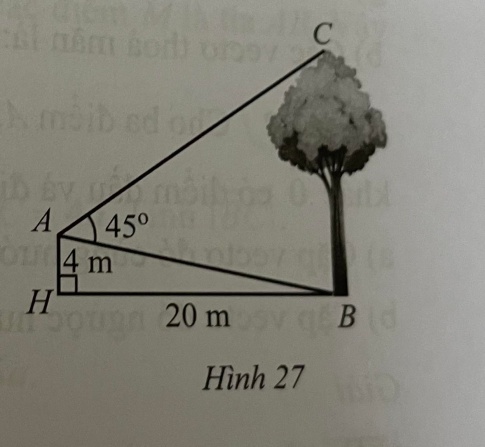
Bài 21 : Một người đứng ở vị trí A trên nóc của một ngôi nhà cao 4m đang quan sát một cây cao cách ngôi nhà 20 m và đo được BAC^=45°">BAC^=45°">BAC^=45°">BAC^=45°">BAC^=45°">BAC^=45°">góc BBAC^=45°">ABAC^=45°">C BAC^=45°">= BAC^=45°">45BAC^=45°">°BAC^=45°">(Hình 27). Tính chiều cao của cây đó (làm tròn kết quả đến hàng phần mười theo đơn vị mét).