Giải bài tập chuyên đề toán lớp 10 chân trời sáng tạo bài 1 phương pháp quy nạp toán học
Hướng dẫn giải chuyên đề bài 1 phương pháp quy nạp toán học từ sách Giải bài tập chuyên đề toán lớp 10 chân trời sáng tạo
Bài toán toán học luôn là một thách thức đối với học sinh, nhất là khi làm về phương pháp quy nạp. Tuy nhiên, sách Giải bài tập chuyên đề toán lớp 10 chân trời sáng tạo đã biên soạn một cách rõ ràng và cụ thể để giúp các em hiểu bài một cách dễ dàng hơn.
Trang 27 của sách chuyên đề này hướng dẫn chi tiết cách giải bài 1 theo phương pháp quy nạp. Những bước thực hiện được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững kiến thức.
Bộ sách này không chỉ giúp học sinh làm quen với bài toán mà còn phát triển năng lực vận dụng trí thức. Hy vọng rằng, qua cách hướng dẫn cụ thể và giải chi tiết trong sách, học sinh sẽ tự tin hơn khi đối diện với các bài toán toán học phức tạp.
Bài tập và hướng dẫn giải
1.PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Hoạt động khám phá: Bằng cách tô màu trên lưới ô vuông như hình dưới đây
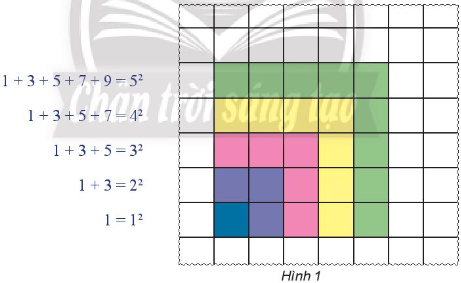
1 + 3 + 5 + 7 +... + (2n – 1) = n2. (1)
a) Hãy chỉ ra công thức (1) đúng với n = 1, 2, 3, 4, 5.
b) Từ việc tô màu trên lưới ô vuông như Hình 1, bạn học sinh khẳng định rằng công thức (1) chắc chắn đúng với mọi số tự nhiên n ≥ 1. Khẳng định như vậy đã thuyết phục chưa? Tại sao?
Thực hành 1: Chứng minh rằng đẳng thức sau đúng với mọi n∈ℕ*">
![]()
Thực hành 2: Chứng minh rằng bất đẳng thức sau đúng với mọi số tự nhiên n ≥ 3: 2n + 1 > n^2 + n + 2
2. ỨNG DỤNG PHƯƠNG PHÁP QUY NẠP TOÁN HỌC
Thực hành 3: Chứng minh rằng n3 + 2n chia hết cho 3 với mọi n∈ℕ*">
Thực hành 4: Chứng minh rằng đẳng thức sau đúng với mọi n∈ℕ*">
![]()
Thực hành 5: Chứng minh rằng trong mặt phẳng, n đường thẳng khác nhau cùng đi qua một điểm chia mặt phẳng thành 2n phần (n∈ℕ*">)
Vận dụng: Một khoản tiền A đồng (gọi là vốn) được gửi tiết kiệm có kì hạn ở một ngân hàng theo thể thức lãi kép (tiền lãi sau mỗi kì hạn nếu không rút ra thì được cộng vào vốn của kì kế tiếp). Giả sử lãi suất theo kì là r không đổi qua các kì hạn, người gửi không rút tiền vốn và lãi trong suốt các kì hạn đề cập sau đây. Gọi Tn là tổng số tiền vốn và lãi của người gửi sau kì hạn thứ n (n∈ℕ*)
a) Tính T1, T2, T3.
b) Từ đó, dự đoán công thức tính Tn và chứng minh công thức đó bằng phương pháp quy nạp toán học.
BÀI TẬP
1.Chứng minh các đẳng thức sau đúng với mọi n∈ℕ*">
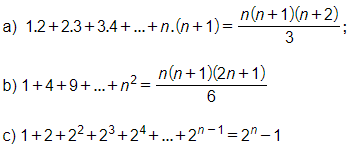
2. Chứng minh rằng, với mọi
n∈ℕ*">n∈ℕ*, ta có:
a) 52n – 1 chia hết cho 24;
b) n3 + 5n chia hết cho 6.
3. Chứng minh rằng nếu x > –1 thì $(1 + x)^n$ ≥ 1 + nx với mọi n∈ℕ*">nn∈ℕ*">∈n∈ℕ*">n∈ℕ*">Nn∈ℕ*">∗
4. Cho a, b ≥ 0. Chứng minh rằng bất đẳng thức sau đúng với mọi n∈ℕ*:">
![]()
5. Chứng minh rằng bất đẳng thức sau đúng với mọi số tự nhiên n ≥ 2:
![]()
6. Trong mặt phẳng, cho đa giác A1 A2 A3... An có n cạnh (n ≥ 3). Gọi Sn là tổng số đo các góc trong của đa giác.
a) Tính S3, S4, S5 tương ứng với trường hợp đa giác là tam giác, tứ giác, ngũ giác.
b) Từ đó, dự đoán công thức tính Sn và chứng minh công thức đó bằng phương pháp
7. Hàng tháng, một người gửi vào ngân hàng một khoản tiền tiết kiệm không đổi a đồng. Giả sử lãi suất hằng tháng là r không đổi và theo thể thức lãi kép (tiền lãi của tháng trước được cộng vào vốn của tháng kế tiếp). Gọi Tn (n ≥ 1) là tổng tiền vốn và lãi của người đó có trong ngân hàng tại thời điểm ngay sau khi gửi vào khoản thứ n + 1.
a) Tính T1, T2, T3.
b) Dự đoán công thức tính Tn và chứng minh công thức đó bằng phương pháp quy nạp toán học.





