Giải bài tập chuyên đề toán lớp 10 chân trời sáng tạo bài 1 elip
Hướng dẫn giải chuyên đề bài 1 elip trang 42, sách chuyên đề toán lớp 10 chân trời sáng tạo
Bài toán elip là một trong những bài toán khá phổ biến và quan trọng trong chương trình toán học. Để giúp các em học sinh hiểu rõ hơn về bài toán này, sách chuyên đề toán lớp 10 chân trời sáng tạo đã biên soạn một cách cụ thể và chi tiết.
Mục tiêu của bộ sách là giúp các em phát triển năng lực vận dụng kiến thức toán học vào thực tế, từ đó nâng cao hiểu biết và kỹ năng giải quyết vấn đề của mình. Việc hướng dẫn và giải thích cặn kẽ sẽ giúp các em nắm bắt bài học hiệu quả hơn và tự tin hơn khi giải các bài tập tương tự.
Hy vọng rằng, với sự hỗ trợ từ sách chuyên đề toán lớp 10 chân trời sáng tạo, các em sẽ có cơ hội tiếp cận và thực hành những bài toán thú vị và bổ ích, từ đó phát triển tư duy logic và khám phá sự hấp dẫn của môn toán.
Bài tập và hướng dẫn giải
1. TÍNH ĐỐI XỨNG CỦA ELIP
Hoạt động khám phá 1: Cho elip (E) có phương trình chính tắc
$\frac{x^2}{a^2}$ + $\frac{y^2}{b^2}$=1
(0<b<a) và cho điểm M(x0; y0) nằm trên (E).
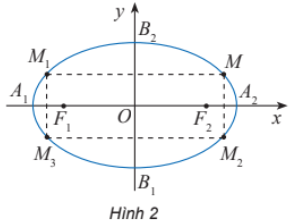
Các điểm M1(–x0; y0), M2(x0; –y0), M3(–x0; –y0) có thuộc (E) hay không?
1. TÍNH ĐỐI XỨNG CỦA ELIP
Hoạt động khám phá 1: Cho elip (E) có phương trình chính tắc
$\frac{x^2}{a^2}$ + $\frac{y^2}{b^2}$=1
(0<b<a) và cho điểm M(x0; y0) nằm trên (E).

Các điểm M1(–x0; y0), M2(x0; –y0), M3(–x0; –y0) có thuộc (E) hay không?
Thực hành 1: Viết phương trình chính tắc của elip có kích thước của hình chữ nhật cơ sở là 8 và 6. Hãy xác định tọa độ đỉnh, tiêu điểm, tiêu cự, độ dài trục của elip này.
Vận dụng 1: Hãy gấp một mảnh giấy hình elip thành bốn phần chồng khít lên nhau.
2. BÁN KÍNH QUA TIÊU
Hoạt động khám phá: Cho điểm M(x; y) nằm trên elip (E):
$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1 có hai tiêu điểm là F1(–c; 0), F2(c; 0) (Hình 6)
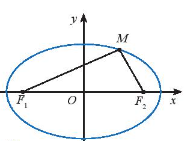
a) Tính $F1M^2$và $F2M^2 $ theo x, y, c.
b, Chứng tỏ rằng: $F1M^2$-$F2M^2$=4cx, F1M-F2M=2$\frac{cx}{a}$
Thực hành 2:
a, Tính độ dài hai bán kính qua tiêu của điểm M(x,y) trên elip (E):
$\frac{x^2}{64}$ + $\frac{y^2}{36}$ = 1
b, Tìm các điểm trên elip (E): $\frac{x^2}{a^2}$ + $\frac{y^2}{b^2}$ = 1
có độ dài hai bán kính qua tiêu bằng nhau.
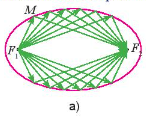
Vận dụng 2: Người ta chứng minh được rằng nếu ánh sáng hay âm thanh đi từ một tiêu điểm, khi đến một điểm M bất kì trên elip luôn luôn cho tia phản xạ đi qua tiêu điểm còn lại, nghĩa là đi theo các bán kính qua tiêu điểm (Hình 7a)
Vòm xe điện ngầm của một thành phố có mặt cắt hình elip (Hình 7b). Hãy giải thích tại sao tiếng nói của một người phát ra từ một tiêu điểm bên này, mặc dù khi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc
3. TÂM SAI
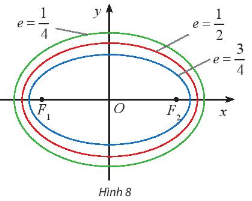
Hoạt động khám phá 3: Cho biết tỉ số e=$\frac{c}{a}$ của các elip lần lượt là $\frac{3}{4}$, $\frac{1}{2}$, $\frac{1}{4}$ (Hình 8)
Tính tỉ số $\frac{a}{b}$ theo e và nêu nhận xét về sự thay đổi của hình dạng elip gắn với hình chữ nhật cơ sở khi e thay đổi.
Thực hành 3:
a, Tìm tâm sai của elip (E): $\frac{x^2}{100}$ + $\frac{y^2}{99}$ = 1 và elip
(E′): $\frac{x^2}{10}$ + $\frac{y^2}{1}$ = 1
b, Không cần vẽ hình, theo bạn elip nào có hình dạng "dẹt" hơn?
Vận dụng 3: TRong hệ mặt trời, các hành tinh chuyển động theo quỹ đạo là đường elip nhận tâm mặt trời là một tiêu điểm. Từ hình ảnh mô phỏng quỹ đạo chuyên động của các hành tinh (Hình 9), hãy so sánh tâm sai của quỹ đạo chuyển động của trái đât với tâm sai của quỹ đạo chuyển động của tiểu hành tinh HD20782b.
4. ĐƯỜNG CHUẨN
Hoạt động khám phá 4: Cho điểm M(x; y) trên elip (E):
$\frac{x^2}{a^2}$ + $\frac{x^2}{100}$ = 1 và hai đường thẳng Δ1= x+$\frac{c}{a}$ =0
Δ1= x-$\frac{c}{a}$=0 (Hình 10). Gọi d(M; Δ1), d(M; Δ2) lần lượt là khoảng cách từ M đến Δ1, Δ2. Ta có (M;Δ1)=$\left \| x+\frac{a}{e} \right \|$=![]()
(vì e > 0 và a+e⁢x=M⁢F1>0">a+ex=MF1>0a+ex=MF1>0). Suy ra
![]()
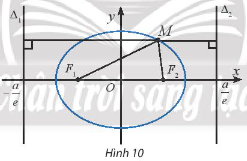
Dựa theo cách tính trên, hãy tính $\frac{MF2}{d(M,\Delta 2)}$
Thực hành 4: Tìm tọa độ hai tiêu điểm và viết phương trình hai đường chuẩn tương ứng của các elip sau:
a, (E1): $\frac{x^2}{4}$ + $\frac{y^2}{1}$
b, (E2): $\frac{x^2}{100}$ + $\frac{y^2}{36}$
Vận dụng 4: Lập phương trình chính tắc của elip có tiêu cự bằng 6 khoảng cách giữa hai đường chuẩn là $\frac{50}{3}$
BÀI TẬP
Bài tập 1: Cho elip (E): $\frac{x^2}{64}$ + $\frac{x^2}{36}$ = 1
a, Tìm tâm sau, chiều dài, chiều rộng hình chữ nhật có sở của (E) và vẽ (E)
b, Tìm độ dài hai bán kính qua tiêu điểm của M(0.6) trên (E)
c, Tìm tọa độ hai tiêu điểm và viết phương trình hai đường chuẩn của (E)
Bài tập 2: Tìm các điểm trên elip (E): $\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1 có độ dài hai bán kính qua tiêu nhỏ nhất, lớn nhất
Bài tập 3: Lập phương trìn chính tắc của elip có tiêu cự bằng 12 và khoảng cách giữa hai đường chuẩn là $\frac{169}{6}$
Bài tập 4: Cho elip (E):
$\frac{x^2}{9}$ + $\frac{x^2}{1}$ = 1
a) Tìm tâm sai và độ dài hai bán kính qua tiêu của điểm M(3; 0) trên (E).
b) Tìm điểm N trên (E) sao cho NF1 = NF2.
c) Tìm điểm S trên (E) sao cho SF1 = 2SF2.
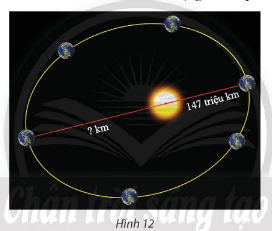
Bài tập 5: Trái Đất chuyển động theo một quỹ đạo là đường elip có tâm sai là 0,0167 và nhận tâm Mặt Trời là một tiêu điểm. Cho biết khoảng cách gần nhất giữa Trái Đất và tâm Mặt Trời là khoảng 147 triệu km, tính khoảng cách xa nhất giữa Trái Đất và tâm Mặt Trời.
Bài tập 6: Ngày 04/10/1957, Liên Xô đã phóng thành công vệ tinh nhân tạo đầu tiên vào không gian, vệ tinh mang tên Sputnik I. Vệ tinh đó có quỹ đạo hình elip (E) nhận tâm Trái Đất là một tiêu điểm. Cho biết khoảng cách xa nhất giữa vệ tinh và tâm Trái Đất là 7310 km và khoảng cách gần nhất giữa vệ tinh và tâm Trái Đất là 6586 km. Tìm tâm sai của quỹ đạo chuyển động của vệ tinh Sputnik I.

Thực hành 1: Viết phương trình chính tắc của hypebol có kích thước của hình chữ nhật cơ sở là 8 và 6. Xác định đỉnh, tiêu điểm, tiêu cự, độ dài trục của hypebol này.




